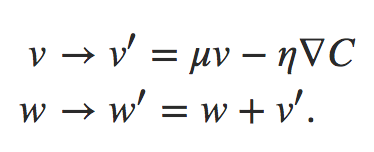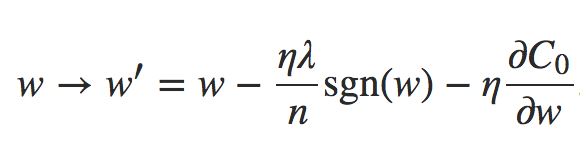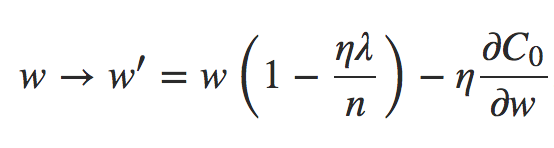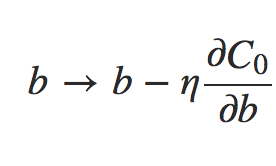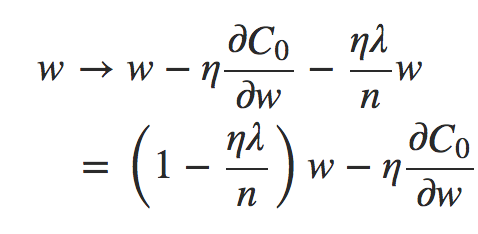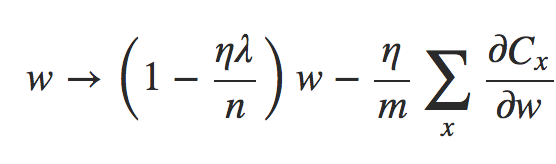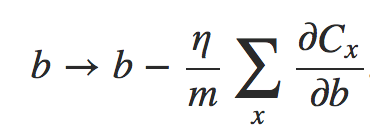Capítulo 76 – O Que é BERT (Bidirectional Encoder Representations from Transformers)?
BERT (Bidirectional Encoder Representations from Transformers) é o algoritmo de aprendizado profundo (Deep Learning) do Google para PLN (Processamento de Linguagem Natural). Ajuda computadores e máquinas a entender a linguagem como nós, humanos, fazemos. Simplificando, o BERT pode ajudar o Google a entender melhor o significado das palavras nas consultas no mecanismo de busca.
Por exemplo, nas frases “quinze para as seis” e “nove para as seis”, a preposição “para” é interpretada de uma maneira diferente pelos humanos em comparação com um motor de busca que a trata como um só. O BERT permite que os mecanismos de busca entendam essas diferenças para fornecer resultados de pesquisa mais relevantes aos usuários.
Desenvolvido no ano de 2018, o BERT é um modelo pré-treinado para Processamento de Linguagem Natural, de código aberto (open-source). Agora, ele pode ser usado por qualquer pessoa para treinar seus sistemas de processamento de linguagem. Para facilitar as melhores consultas de pesquisa, ele é construído em representações contextuais de pré-treinamento, como o Transformer, ULMFiT, o transformador OpenAI, Semi-Supervised Sequence Learning e Elmo.
Um ponto importante de diferença entre o BERT e outros modelos de PLN é que é a primeira tentativa do Google de um modelo pré-treinado que é profundamente bidirecional e faz pouco uso de qualquer outra coisa além de um corpus de texto simples. Como é um modelo de código aberto, qualquer pessoa com conhecimento sólido de algoritmos de aprendizado de máquina pode usá-lo para desenvolver um modelo de PLN sem ter que integrar conjuntos de dados diferentes para treinamento de modelo, economizando recursos e dinheiro.
Outro diferencial importante em relação ao BERT é que ele foi pré-treinado em um corpus gigantesco de texto que ultrapassa 33 milhões de itens.
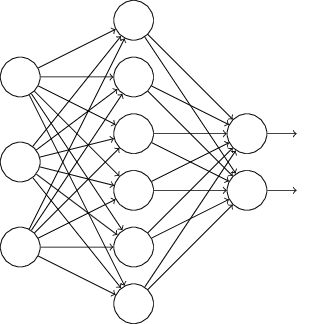
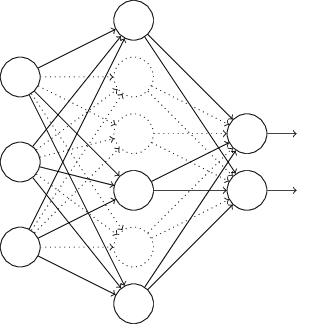
O Que é Uma Rede Neural?
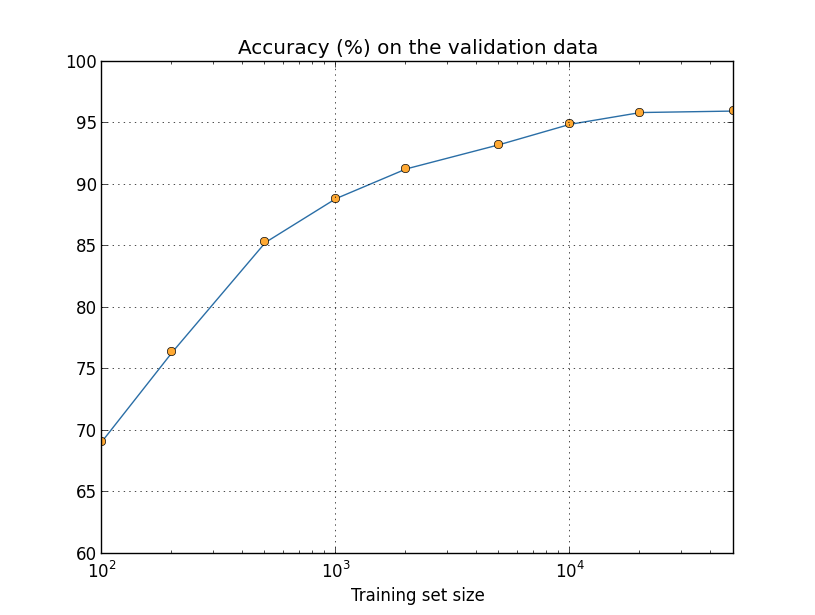
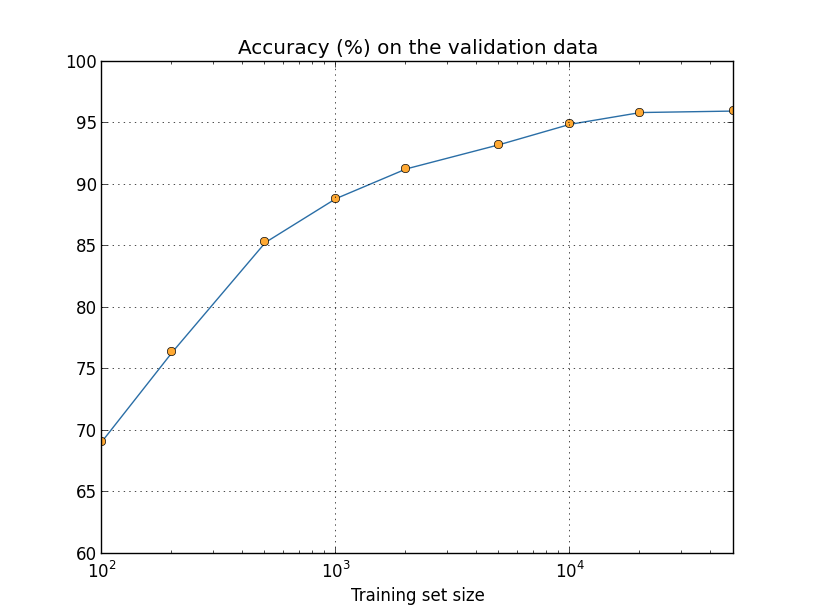
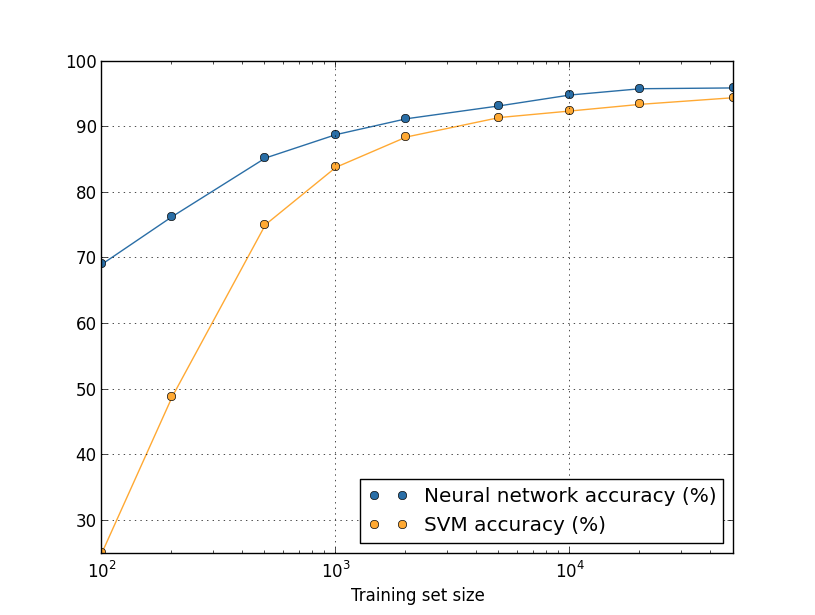
Conforme vimos nos capítulos deste livro, algoritmos projetados para redes neurais funcionam identificando ou reconhecendo padrões. Prever tendências globais no domínio econômico, classificar o conteúdo da imagem e identificar a caligrafia são algumas das aplicações comuns das redes neurais no mundo real. Elas empregam conjuntos de dados para reconhecimento de padrões. Na verdade, o BERT foi pré-treinado na Wikipedia que ultrapassa 2500 milhões de palavras.
O Que é Processamento de Linguagem Natural?
O Processamento de Linguagem Natural (PLN) é um ramo da Inteligência Artificial projetado para ajudar as máquinas a entender o processo natural de comunicação dos seres humanos.
Você digita uma palavra na caixa de pesquisa do Google e uma série de sugestões aparecem. Você se comunica com chatbots de uma empresa. Todas essas comunicações são possibilitadas via PLN.
Exemplos de avanços possibilitados por PLN incluem ferramentas de escuta social, chatbots e sugestões de palavras em seu smartphone. Embora PLN não seja uma novidade para os mecanismos de pesquisa, o BERT representa um avanço no processamento de linguagem natural por meio do treinamento bidirecional.
Como Funciona o BERT?
Vamos estudar o funcionamento do BERT em mais detalhes no capítulo seguinte, mas o BERT treina os modelos de linguagem com base no conjunto completo de palavras em uma consulta ou frase conhecida como treinamento bidirecional, enquanto os modelos de PLN tradicionais treinam os modelos de linguagem na ordem da sequência de palavras (da direita para a esquerda ou da esquerda para a direita). O BERT facilita os modelos de linguagem a discernir o contexto das palavras com base nas palavras circundantes, em vez de palavras que o seguem ou precedem.
O Google chama esse processo de “profundamente bidirecional” e com razão, pela simples razão de que o verdadeiro significado do que as palavras estão comunicando só é possível por meio de uma análise profunda da rede neural.
Por exemplo, seria difícil para uma máquina diferenciar entre a palavra “banco”, como sendo uma agência bancária, da palavra “banco”, como sendo o local para sentar em uma praça, por exemplo. O modelo contextual funciona mapeando uma representação distinta de toda a frase para entender melhor seus contextos.
O BERT Substituiu o Algoritmo RankBrain?
RankBrain foi o primeiro algoritmo baseado em IA do Google a compreender as consultas de pesquisa e o contexto de uma palavra em uma frase. Ele usa aprendizado de máquina para fornecer os resultados de pesquisa mais relevantes para as consultas do usuário. Corresponde às consultas e ao conteúdo das páginas da web para entender melhor o contexto das palavras em uma frase. É importante compreender que o BERT não foi introduzido como um substituto do RankBrain. Na verdade, ele adiciona mais poder para que os pontos mais precisos do que o usuário está solicitando ou desejando sejam melhor compreendidos e processados. No entanto, se o Google precisa entender melhor o contexto de uma palavra, o BERT certamente se sairá melhor. O Google pode usar vários métodos para entender uma única consulta, incluindo RankBrain e BERT.
No próximo capítulo veremos um pouco dos detalhes técnicos do BERT. Até lá.
Referências:


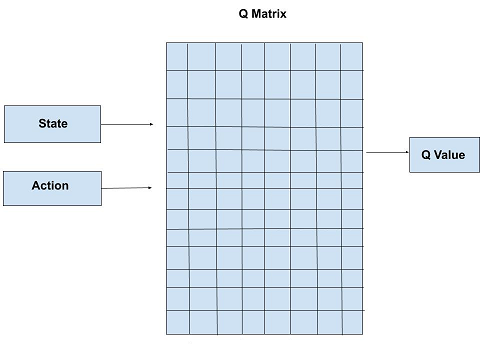
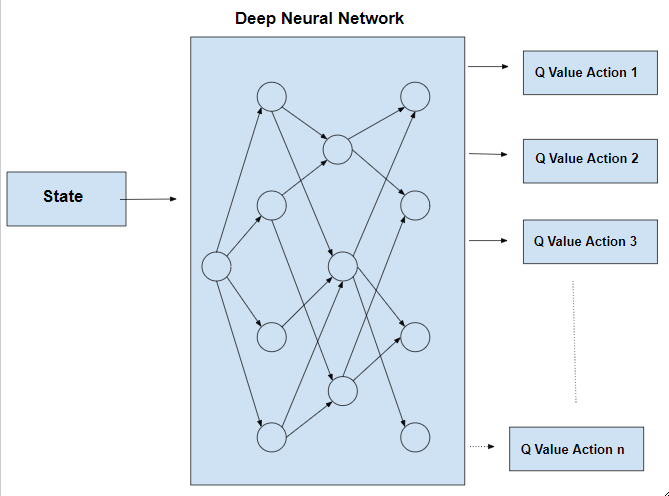

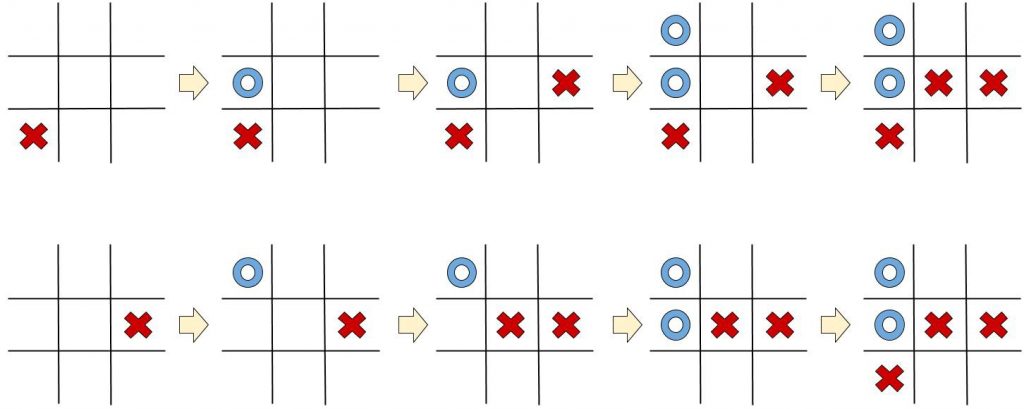
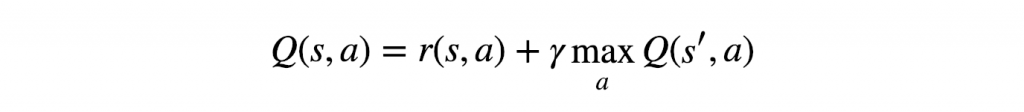
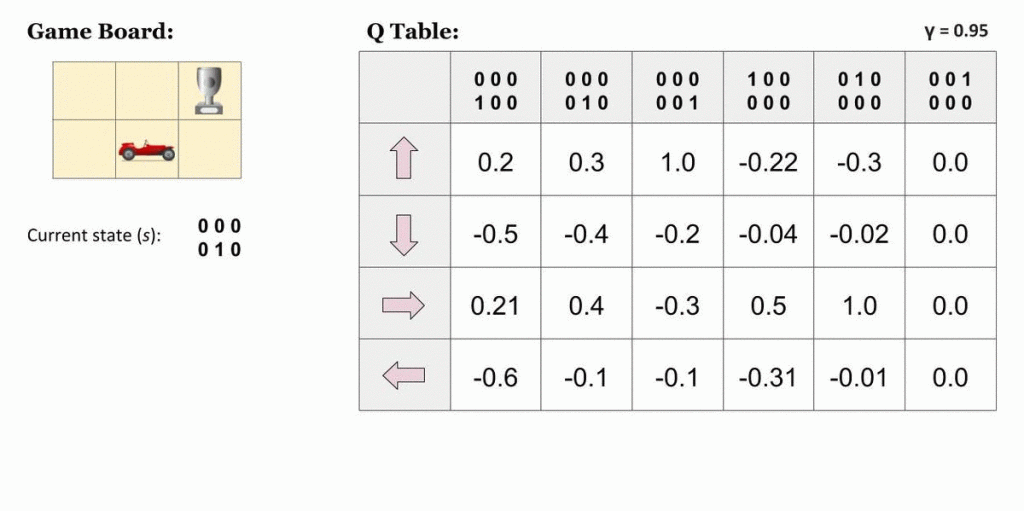
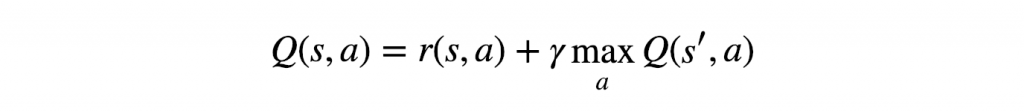
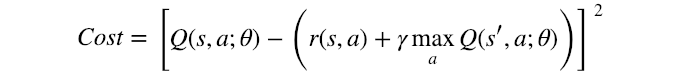







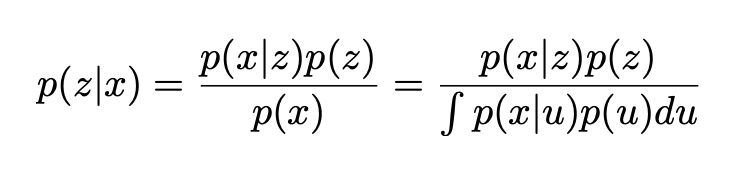
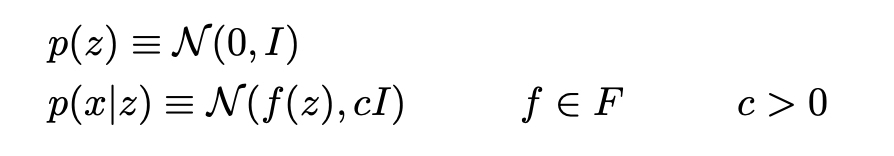
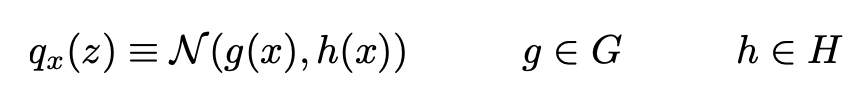
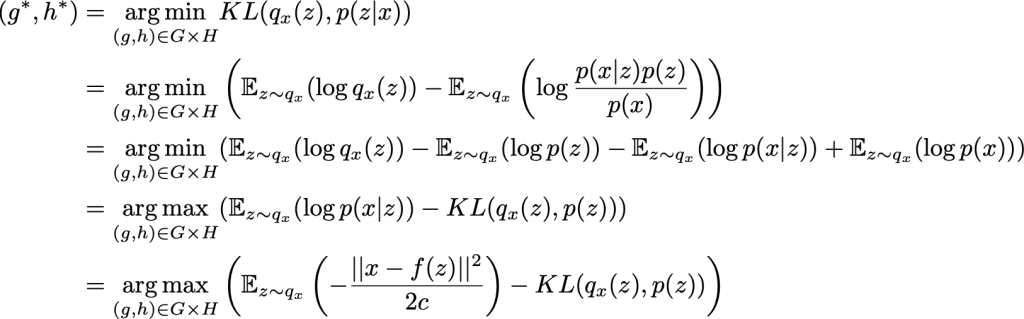
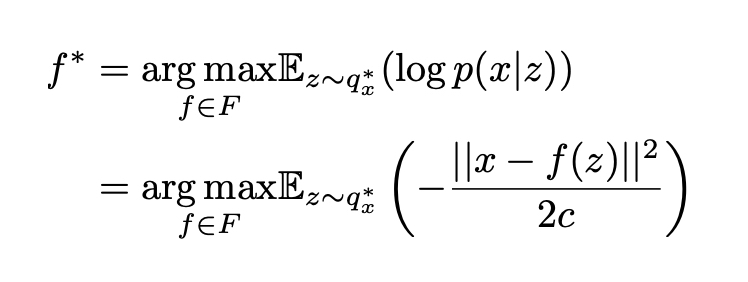
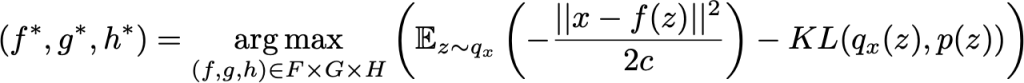
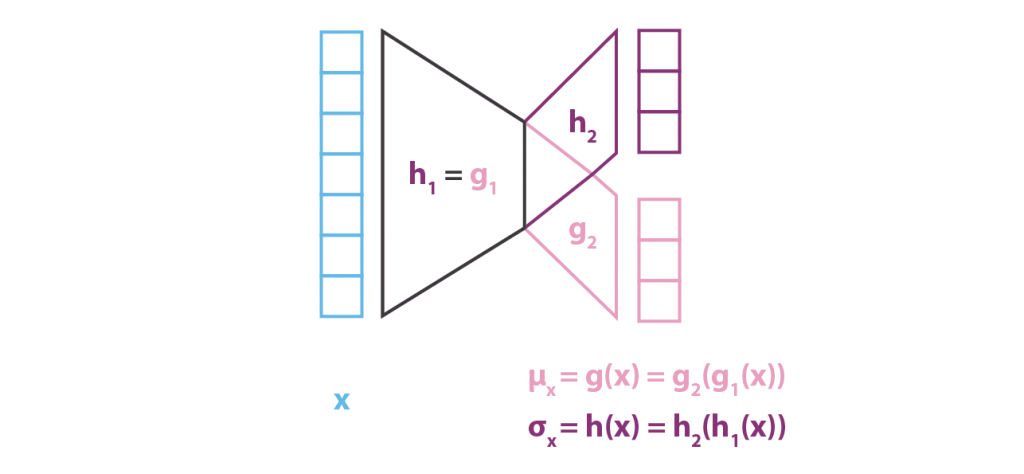
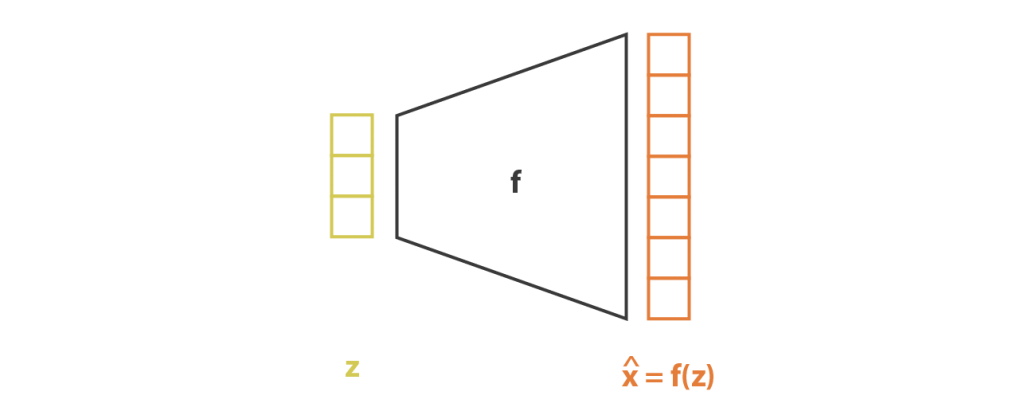
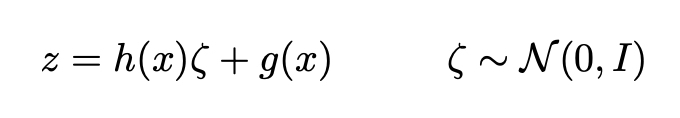
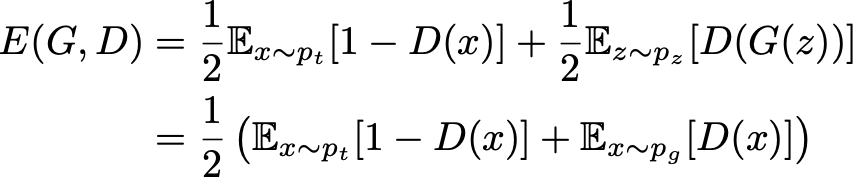
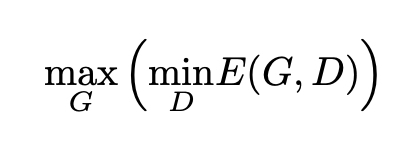
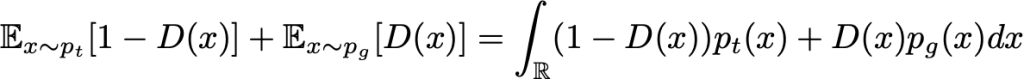
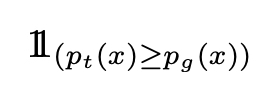
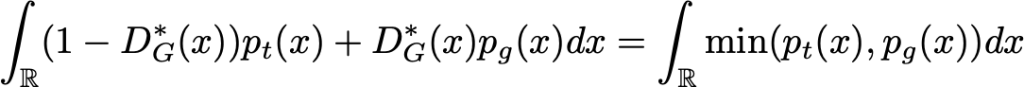
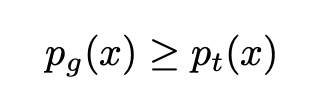
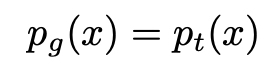
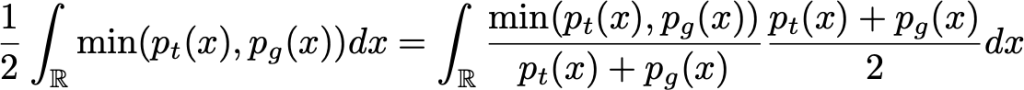



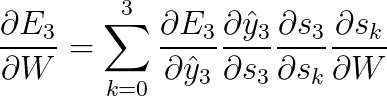
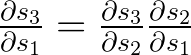
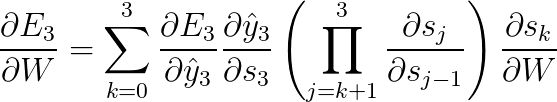
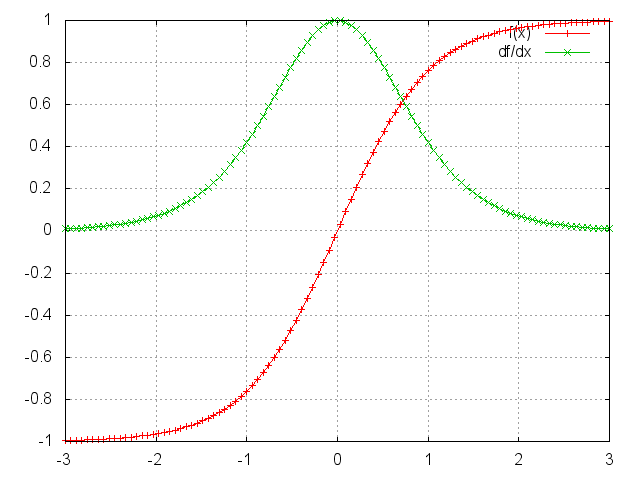
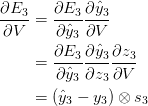
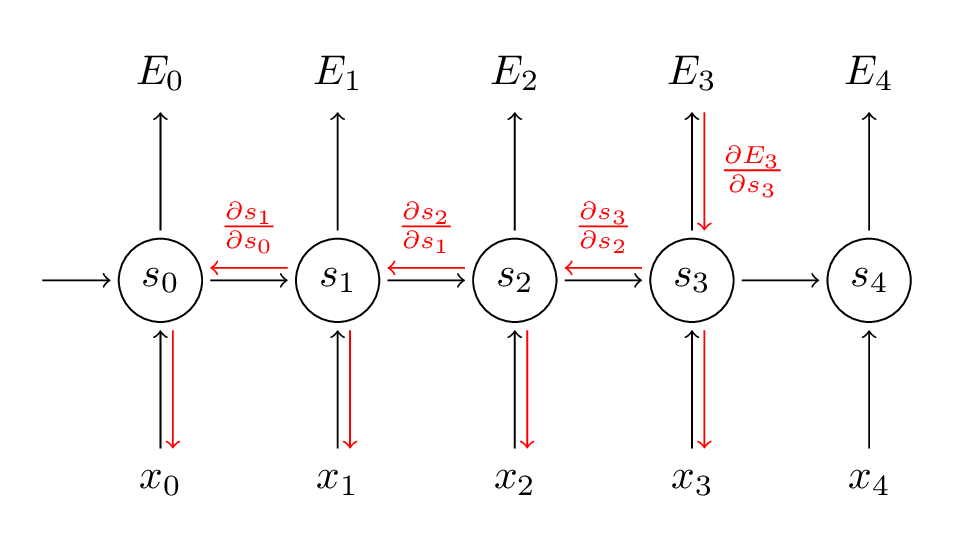
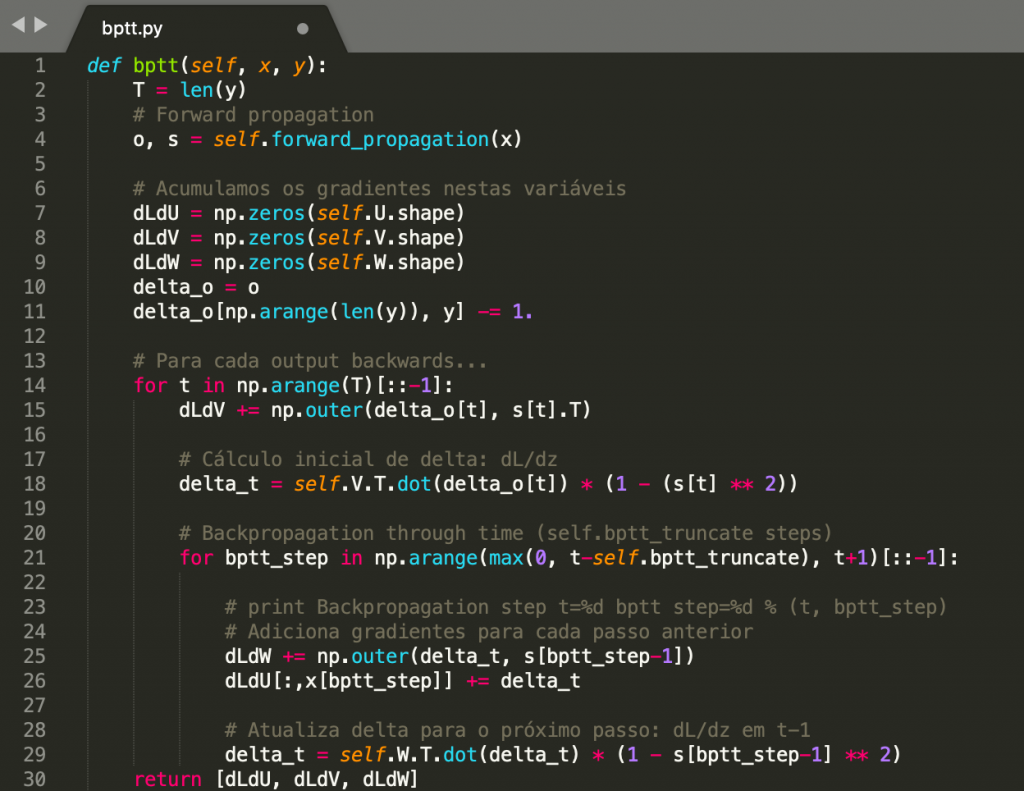



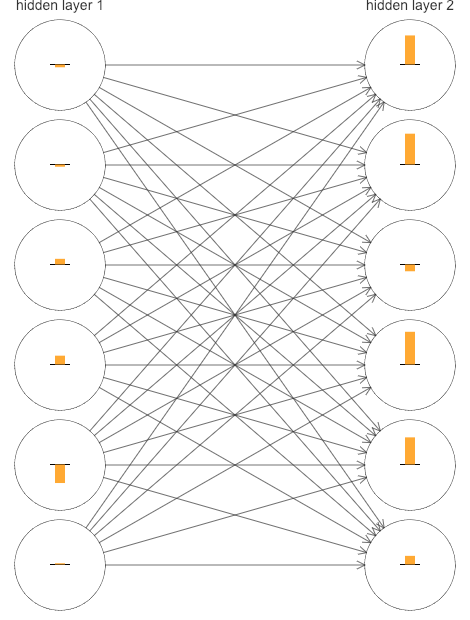

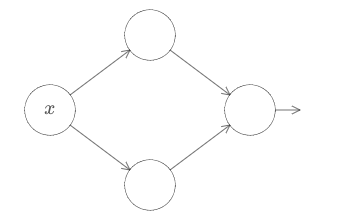
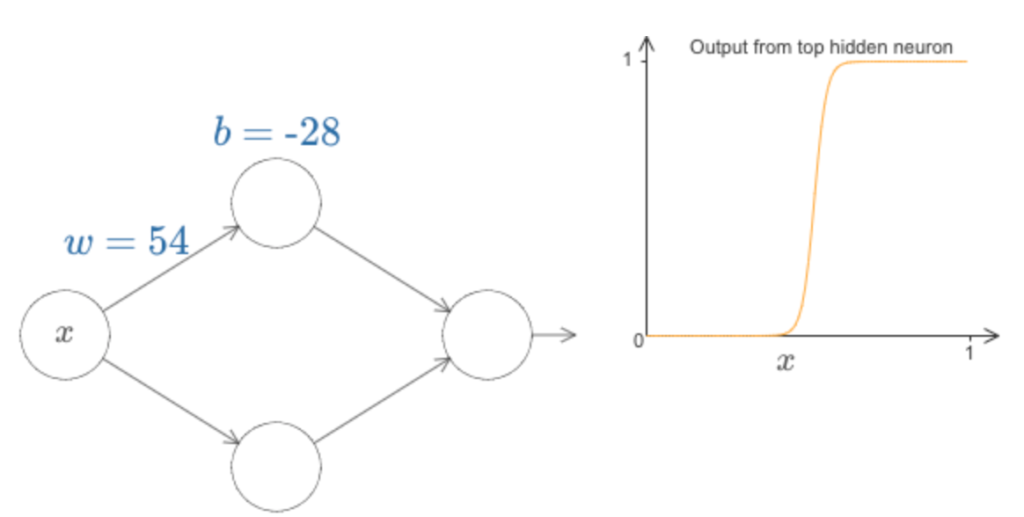
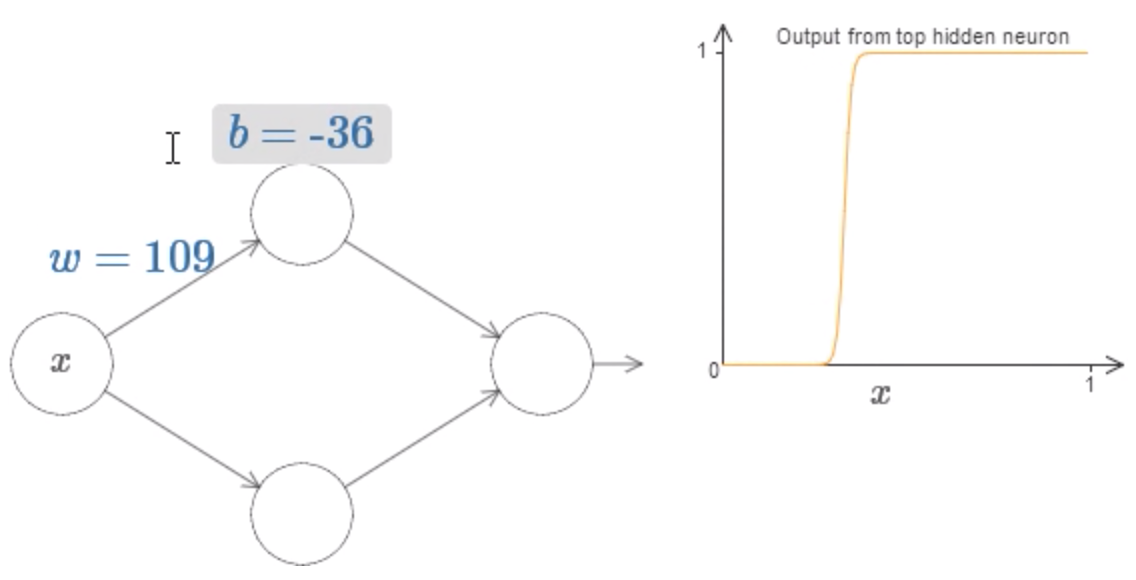
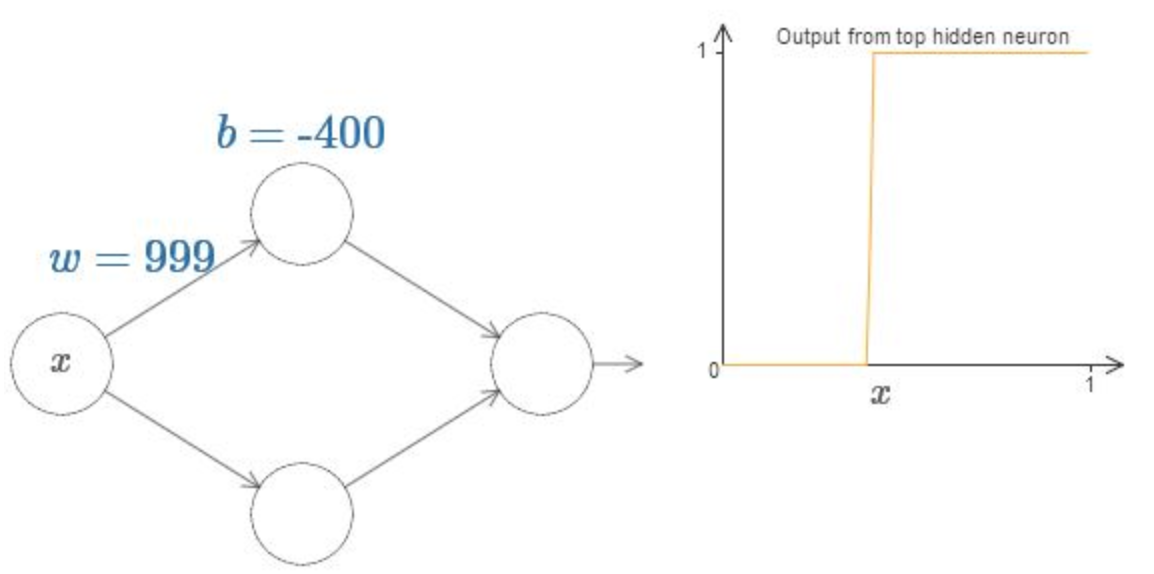
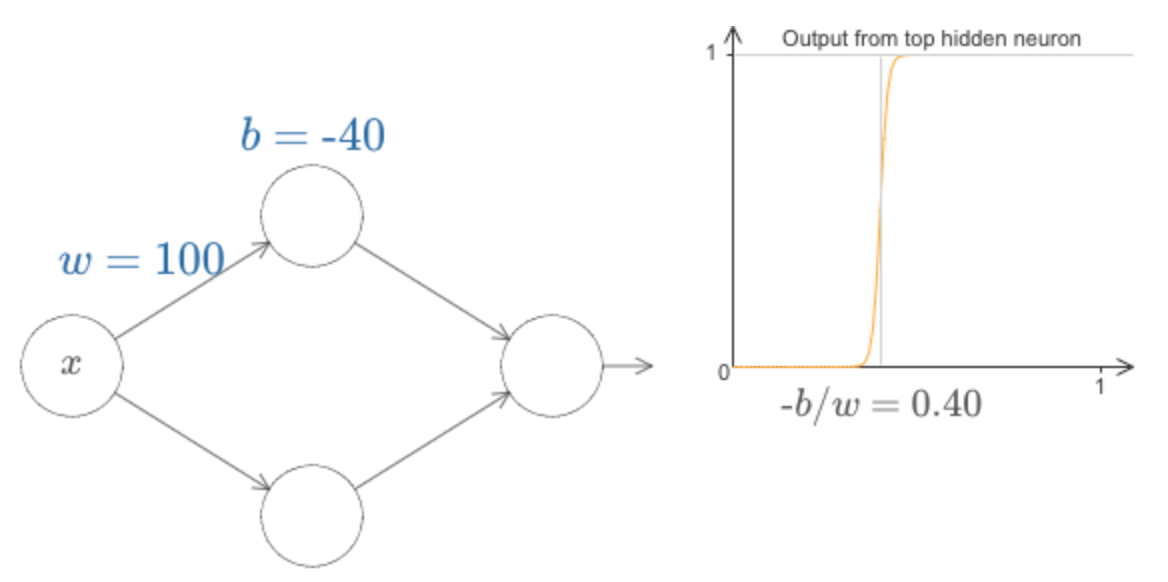
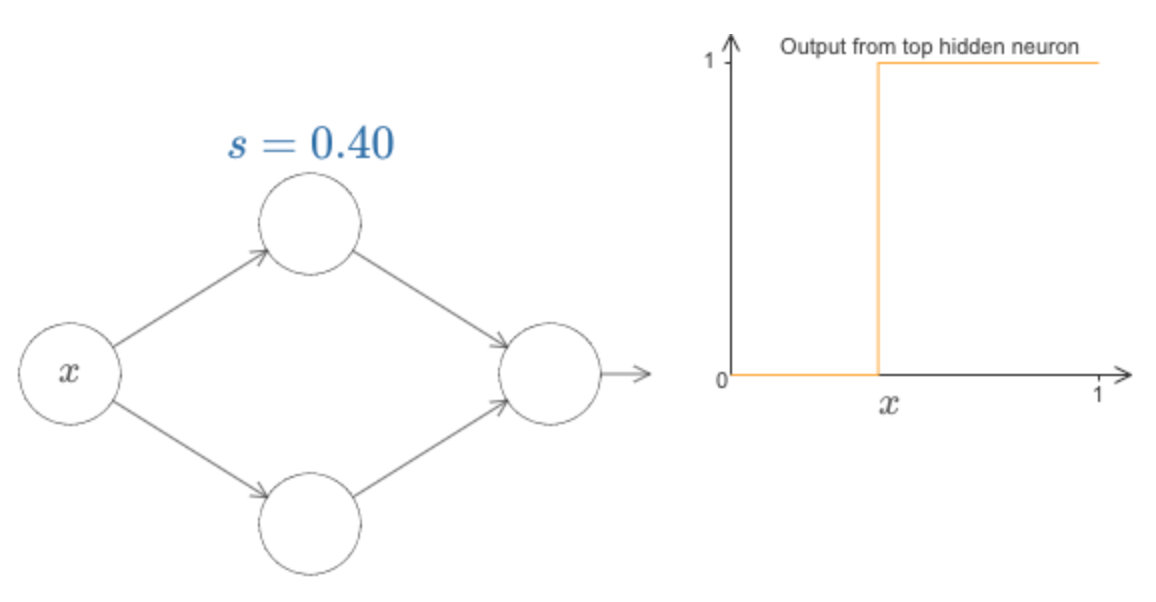
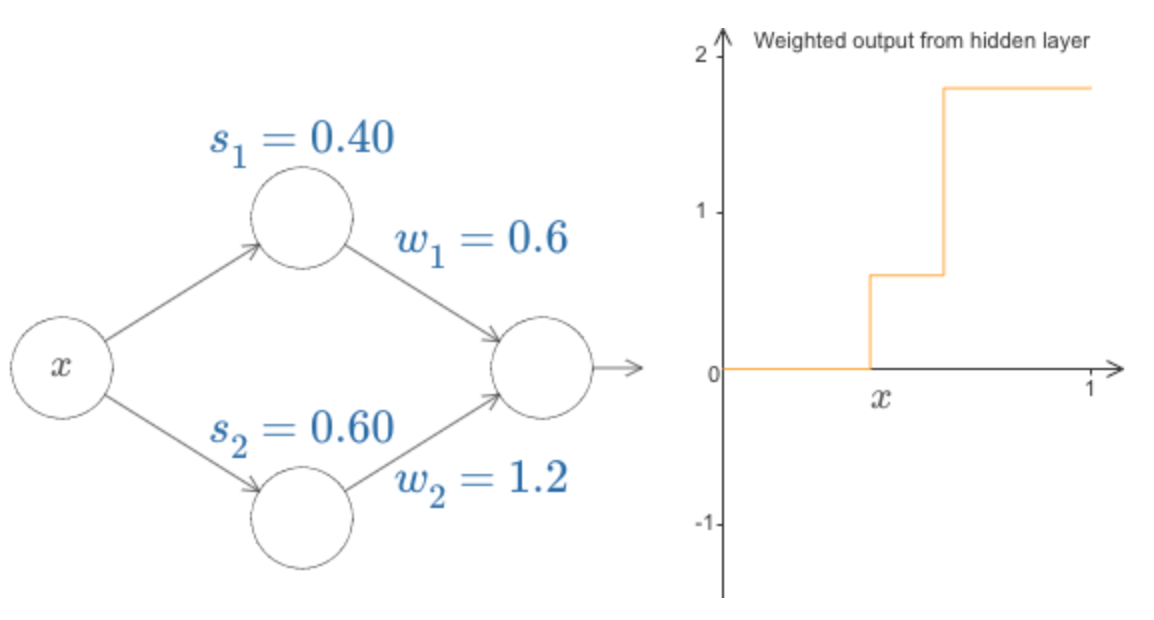
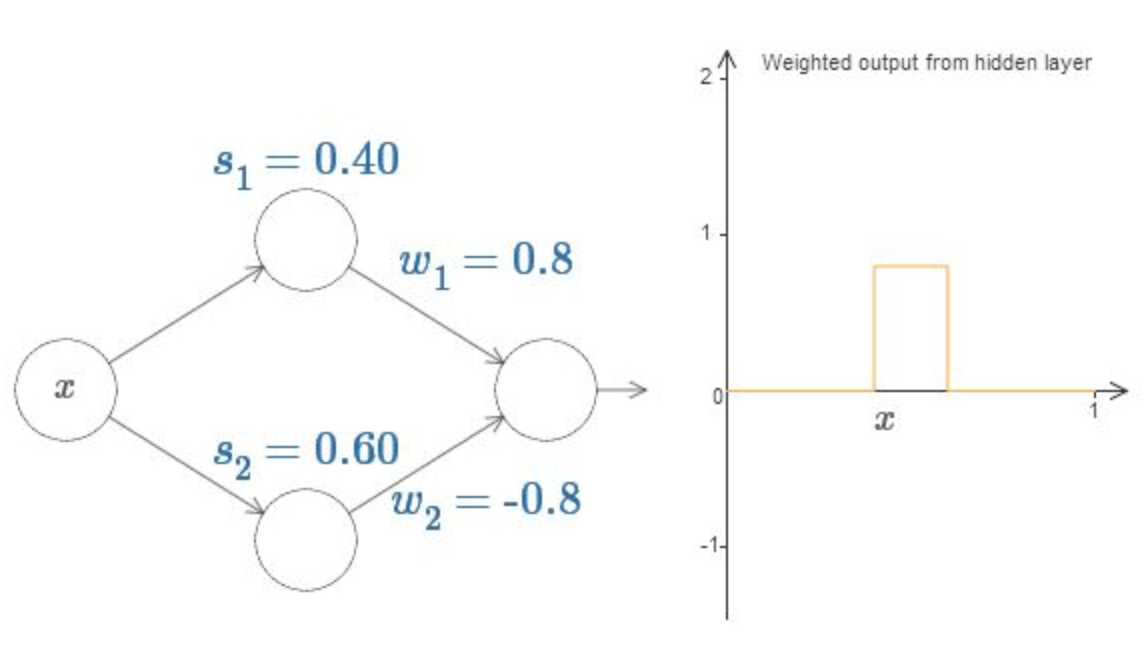

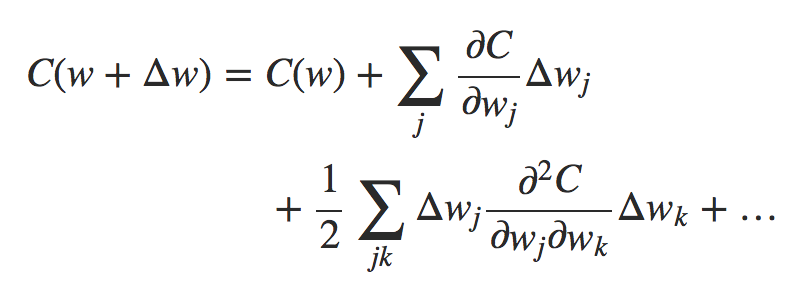
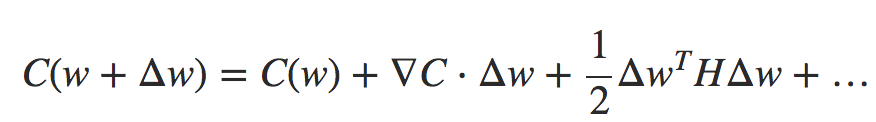
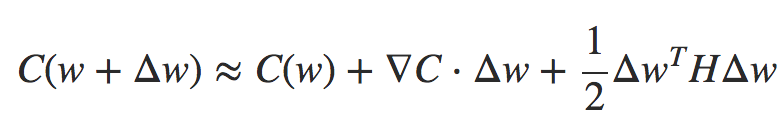
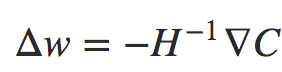
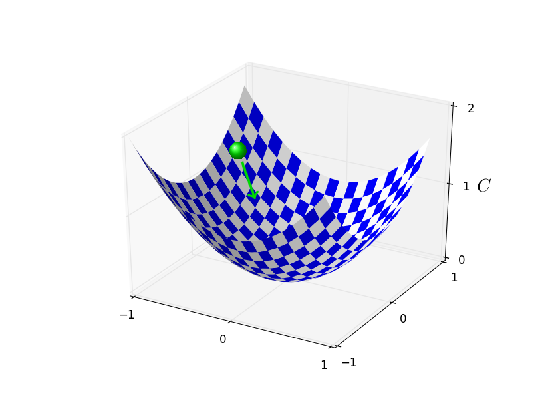
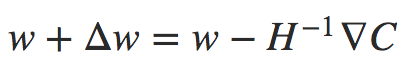 deva diminuir significativamente a função custo. Isso sugere um algoritmo possível para minimizar o custo:
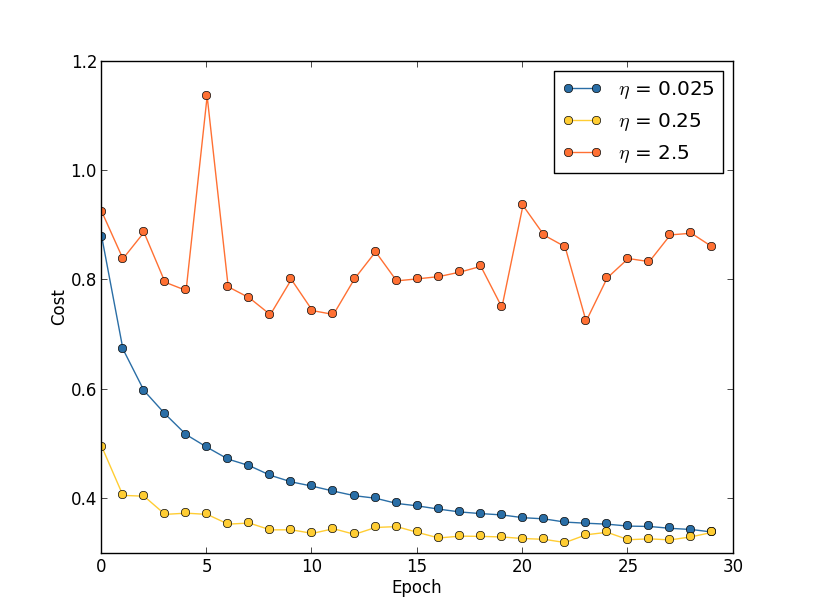
deva diminuir significativamente a função custo. Isso sugere um algoritmo possível para minimizar o custo: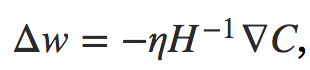 onde η é conhecido como taxa de aprendizado.
onde η é conhecido como taxa de aprendizado.