Capítulo 19 – Overfitting e Regularização – Parte 1
O físico Enrico Fermi, ganhador do Prêmio Nobel de Física em 1938, foi questionado sobre sua opinião em relação a um modelo matemático que alguns colegas haviam proposto como a solução para um importante problema de física não resolvido. O modelo teve excelente performance no experimento, mas Fermi estava cético. Ele perguntou quantos parâmetros livres poderiam ser definidos no modelo. “Quatro” foi a resposta. Fermi respondeu: “Eu lembro que meu amigo Johnny Von Neumann costumava dizer: com quatro parâmetros eu posso encaixar um elefante, e com cinco eu posso fazê-lo mexer seu tronco” *. Com isso, ele quis dizer que não se deve ficar impressionado quando um modelo complexo se ajusta bem a um conjunto de dados. Com parâmetros suficientes, você pode ajustar qualquer conjunto de dados.
(* A citação vem de um artigo de Freeman Dyson, que é uma das pessoas que propôs o modelo. O artigo “Um elefante de quatro parâmetros” ou “A four-parameter elephant” pode ser encontrado aqui.)
O ponto, claro, é que modelos com um grande número de parâmetros podem descrever uma variedade incrivelmente ampla de fenômenos. Mesmo que tal modelo esteja de acordo com os dados disponíveis, isso não o torna um bom modelo. Isso pode significar apenas que há liberdade suficiente no modelo que pode descrever quase qualquer conjunto de dados de tamanho determinado, sem capturar nenhuma percepção genuína do fenômeno em questão. Quando isso acontece, o modelo funcionará bem para os dados existentes, mas não conseguirá generalizar para novas situações. O verdadeiro teste de um modelo é sua capacidade de fazer previsões em situações que não foram expostas antes.
Fermi e von Neumann suspeitavam de modelos com quatro parâmetros. Nossa rede de 30 neurônios ocultos para classificação de dígitos MNIST possui quase 24.000 parâmetros! Nossa rede de 100 neurônios ocultos tem cerca de 80.000 parâmetros e redes neurais profundas de última geração às vezes contêm milhões ou até bilhões de parâmetros. Devemos confiar nos resultados?
Vamos aguçar este problema construindo uma situação em que a nossa rede faz um mau trabalho ao generalizar para novas situações. Usaremos nossa rede de 30 neurônios ocultos, com seus 23.860 parâmetros. Mas não treinamos a rede usando todas as imagens de treinamento de 50.000 dígitos MNIST. Em vez disso, usaremos apenas as primeiras 1.000 imagens de treinamento. Usar esse conjunto restrito tornará o problema com a generalização muito mais evidente. Vamos treinar usando a função de custo de entropia cruzada, com uma taxa de aprendizado de η = 0,5 e um tamanho de mini-lote de 10. No entanto, vamos treinar por 400 épocas, pois não estamos usando muitos exemplos de treinamento. Vamos usar network2 para ver como a função de custo muda (o código você encontra aqui):

Usando os resultados, podemos traçar a maneira como o custo muda à medida que a rede aprende (o script overfitting.py contém o código que gera esse resultado):
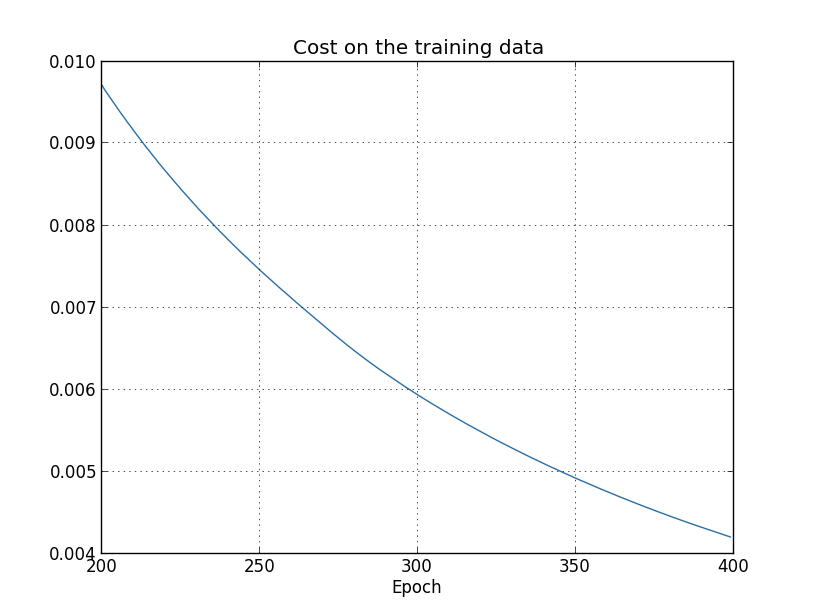
Isso parece encorajador, mostrando uma redução suave no custo, exatamente como esperamos. Note que eu só mostrei as épocas de treinamento de 200 a 399. Isso nos dá uma boa visão dos últimos estágios do aprendizado, que, como veremos, é onde está a ação interessante.
Vamos agora ver como a precisão da classificação nos dados de teste muda com o tempo:
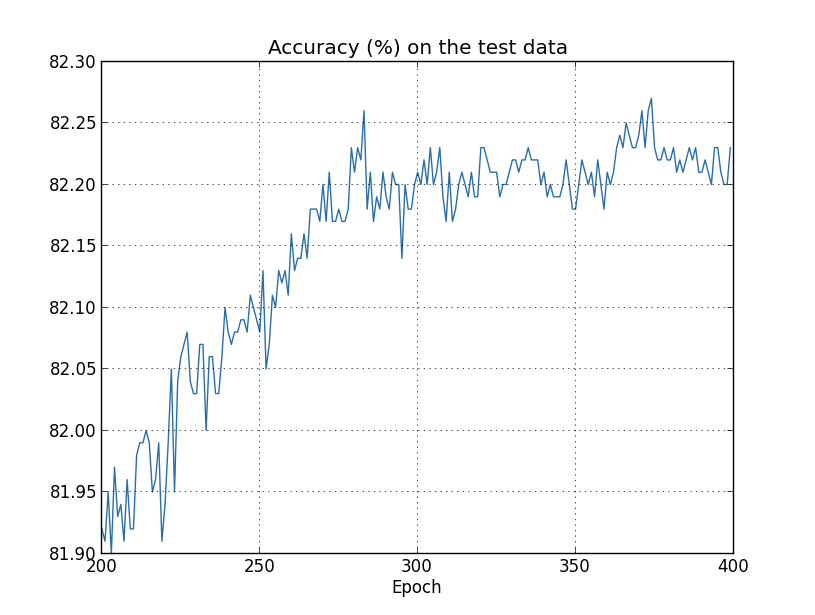
Mais uma vez, eu ampliei um pouco. Nas primeiras 200 épocas (não mostradas), a precisão sobe para pouco menos de 82%. O aprendizado então diminui gradualmente. Finalmente, por volta da época 280, a precisão da classificação praticamente pára de melhorar. As épocas posteriores meramente vêem pequenas flutuações estocásticas perto do valor da precisão na época 280. Compare isso com o gráfico anterior, em que o custo associado aos dados de treinamento continua a cair suavemente. Se olharmos apenas para esse custo, parece que nosso modelo ainda está ficando “melhor”. Mas os resultados da precisão do teste mostram que a melhoria é uma ilusão. Assim como o modelo que Fermi não gostava, o que nossa rede aprende após a época 280 não mais se generaliza para os dados de teste. E assim não é um aprendizado útil. Dizemos que a rede está super adaptando ou com sobreajuste ou ainda com overfitting, a partir da época 280.
Você pode se perguntar se o problema aqui é que eu estou olhando para o custo dos dados de treinamento, ao contrário da precisão da classificação nos dados de teste. Em outras palavras, talvez o problema seja que estamos fazendo uma comparação de maçãs e laranjas. O que aconteceria se comparássemos o custo dos dados de treinamento com o custo dos dados de teste, estaríamos comparando medidas semelhantes? Ou talvez pudéssemos comparar a precisão da classificação tanto nos dados de treinamento quanto nos dados de teste? Na verdade, essencialmente o mesmo fenômeno aparece, não importa como fazemos a comparação. Os detalhes mudam, no entanto. Por exemplo, vamos analisar o custo nos dados de teste:
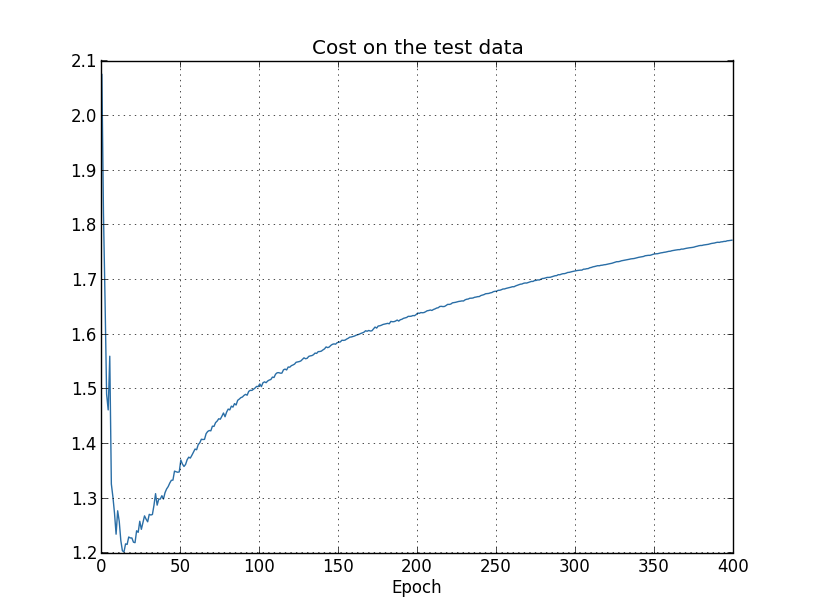
Podemos ver que o custo nos dados de teste melhora até a época 15, mas depois disso ele realmente começa a piorar, mesmo que o custo nos dados de treinamento continue melhorando. Este é outro sinal de que nosso modelo está super adaptando (overfitting). No entanto, coloca um enigma, que é se devemos considerar a época 15 ou a época 280 como o ponto em que o overfitting está dominando a aprendizagem? Do ponto de vista prático, o que realmente nos importa é melhorar a precisão da classificação nos dados de teste, enquanto o custo dos dados de teste não é mais do que um proxy para a precisão da classificação. E assim faz mais sentido considerar a época 280 como o ponto além do qual o overfitting está dominando o aprendizado em nossa rede neural.
Outro sinal de overfitting pode ser visto na precisão da classificação nos dados de treinamento:
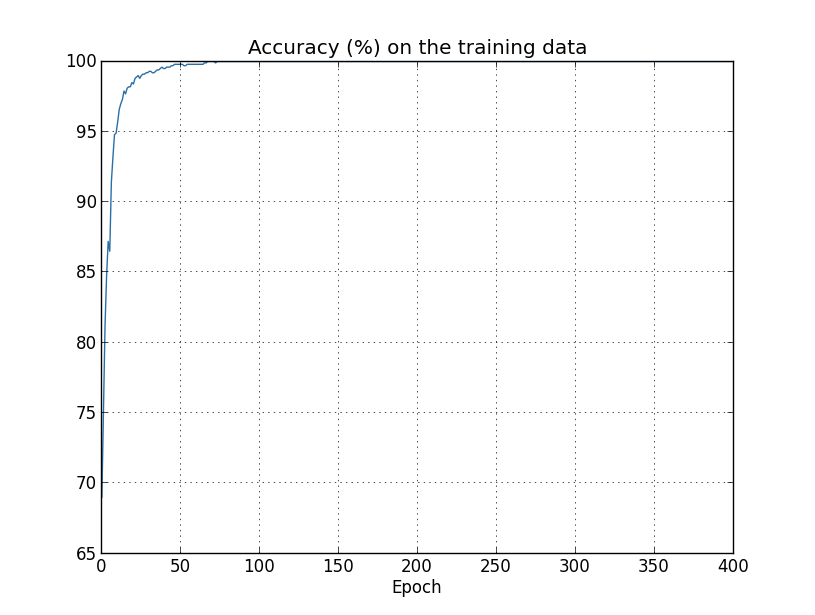
A precisão aumenta até 100%. Ou seja, nossa rede classifica corretamente todas as 1.000 imagens de treinamento! Enquanto isso, nossa precisão de teste atinge apenas 82,27%. Portanto, nossa rede realmente está aprendendo sobre as peculiaridades do conjunto de treinamento, não apenas reconhecendo os dígitos em geral. É quase como se nossa rede estivesse apenas memorizando o conjunto de treinamento, sem entender os dígitos suficientemente bem para generalizar o conjunto de testes.
Overfitting é um grande problema em redes neurais. Isso é especialmente verdadeiro em redes modernas, que geralmente têm um grande número de pesos e vieses. Para treinar de forma eficaz, precisamos de uma maneira de detectar quando o overfitting está acontecendo. E precisamos aplicar técnicas para reduzir os efeitos do overfitting (por todo esse trabalho e conhecimento necessário, Cientistas de Dados devem ser muito bem remunerados).
A maneira óbvia de detectar overfitting é usar a abordagem acima, mantendo o controle da precisão nos dados de teste conforme nossos treinos da rede. Se percebermos que a precisão nos dados de teste não está mais melhorando, devemos parar de treinar. É claro que, estritamente falando, isso não é necessariamente um sinal de overfitting. Pode ser que a precisão nos dados de teste e os dados de treinamento parem de melhorar ao mesmo tempo. Ainda assim, a adoção dessa estratégia impedirá o overfitting.
Na verdade, usaremos uma variação dessa estratégia. Lembre-se de que, quando carregamos os dados MNIST, carregamos em três conjuntos de dados:

Até agora, usamos o training_data e test_data e ignoramos o validation_data. O validation_data contém 10.000 imagens de dígitos, imagens que são diferentes das 50.000 imagens no conjunto de treinamento MNIST e das 10.000 imagens no conjunto de teste MNIST. Em vez de usar o test_data para evitar overfitting, usaremos o validation_data. Para fazer isso, usaremos praticamente a mesma estratégia descrita acima para o test_data. Ou seja, calcularemos a precisão da classificação nos dados de validação no final de cada época. Quando a precisão da classificação nos dados de validação estiver saturada, paramos de treinar. Essa estratégia é chamada de parada antecipada (Early-Stopping). É claro que, na prática, não sabemos imediatamente quando a precisão está saturada. Em vez disso, continuamos treinando até termos certeza de que a precisão está saturada.
Por que usar o validation_data para evitar overfitting, em vez de test_data? Na verdade, isso faz parte de uma estratégia mais geral, que é usar o validation_data para avaliar diferentes opções de avaliação de hiperparâmetros, como o número de épocas para treinamento, a taxa de aprendizado, a melhor arquitetura de rede e assim por diante. Usamos essas avaliações para encontrar e definir bons valores para os hiperparâmetros. De fato, embora eu não tenha mencionado isso até agora, isto é, em parte, como chegamos às escolhas de hiperparâmetros feitas anteriormente neste livro. (Mais sobre isso depois.)
Claro, isso não responde de forma alguma à pergunta de por que estamos usando o validation_data para evitar overfitting, em vez de test_data. Para entender o porquê, considere que, ao definir os hiperparâmetros, é provável que tentemos muitas opções diferentes para os hiperparâmetros. Se definirmos os hiperparâmetros com base nas avaliações do test_data, será possível acabarmos super adequando nossos hiperparâmetros ao test_data. Ou seja, podemos acabar encontrando hiperparâmetros que se encaixam em peculiaridades particulares dos dados de teste, mas onde o desempenho da rede não se generalizará para outros conjuntos de dados. Protegemos contra isso descobrindo os hiperparâmetros usando o validation_data. Então, uma vez que tenhamos os hiperparâmetros que queremos, fazemos uma avaliação final da precisão usando o test_data. Isso nos dá confiança de que nossos resultados nos dados de teste são uma medida real de quão bem nossa rede neural se generaliza. Para colocar de outra forma, você pode pensar nos dados de validação como um tipo de dados de treinamento que nos ajuda a aprender bons parâmetros. Essa abordagem para encontrar bons hiperparâmetros é às vezes conhecida como o método “hold out”, uma vez que os dados de validação são mantidos separados ou “mantidos” a partir dos dados de treinamento.
Agora, na prática, mesmo depois de avaliar o desempenho nos dados de teste, podemos mudar nossa opinião e tentar outra abordagem – talvez uma arquitetura de rede diferente – que envolva a descoberta de um novo conjunto de hiperparâmetros. Se fizermos isso, não há perigo de acabarmos com o test_data também? Precisamos de uma regressão potencialmente infinita de conjuntos de dados, para que possamos ter certeza de que nossos resultados serão generalizados? Abordar essa preocupação é um problema profundo e difícil. Mas para nossos objetivos práticos, não vamos nos preocupar muito com essa questão. Em vez disso, vamos nos concentrar no método básico de retenção, com base nos dados training_data, validation_data e test_data, conforme descrito acima.
Vimos que o overfitting ocorre quando estamos usando apenas 1.000 imagens de treinamento. O que acontece quando usamos o conjunto completo de treinamento de 50.000 imagens? Manteremos todos os outros parâmetros iguais (30 neurônios ocultos, taxa de aprendizado de 0,5, tamanho de mini-lote de 10), mas treinamos usando todas as 50.000 imagens por 30 épocas. Aqui está um gráfico mostrando os resultados da precisão de classificação nos dados de treinamento e nos dados de teste. Observe que usei os dados de teste aqui, em vez dos dados de validação, para tornar os resultados mais diretamente comparáveis aos gráficos anteriores.
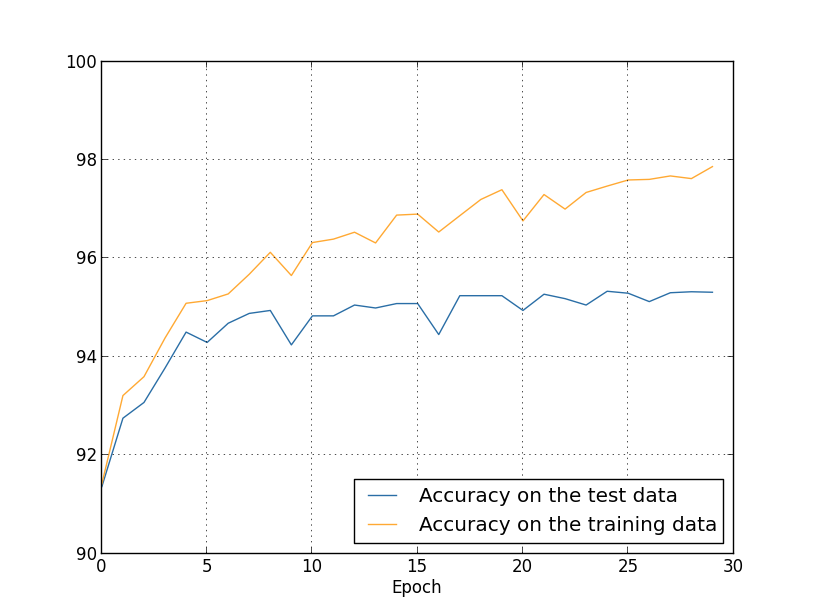
Como você pode ver, a precisão nos dados de teste e treinamento permanece muito mais próxima do que quando estávamos usando 1.000 exemplos de treinamento. Em particular, a melhor precisão de classificação de 97,86% nos dados de treinamento é apenas 2,53% maior do que os 95,33% nos dados de teste. Isso é comparado com a diferença de 17,73% que tivemos anteriormente! Overfitting ainda está acontecendo, mas foi bastante reduzido. Nossa rede está se generalizando muito melhor dos dados de treinamento para os dados de teste. Em geral, uma das melhores maneiras de reduzir o overfitting é aumentar o volume (tamanho) dos dados de treinamento (fica claro agora porque Big Data está revolucionando a Ciência de Dados?). Com dados de treinamento suficientes, é difícil até mesmo uma rede muito grande sofrer de overfitting. Infelizmente, os dados de treinamento podem ser caros ou difíceis de adquirir, por isso nem sempre é uma opção prática.
Aumentar a quantidade de dados de treinamento é uma maneira de reduzir o overfitting. Mas existem outras maneiras de reduzir a extensão do overfitting? Uma abordagem possível é reduzir o tamanho da nossa rede. No entanto, redes grandes têm o potencial de serem mais poderosas do que redes pequenas e, portanto, essa é uma opção que só adotamos em último caso.
Felizmente, existem outras técnicas que podem reduzir o overfitting, mesmo quando temos uma rede fixa e dados de treinamento fixos. Estas técnicas são conhecidas como técnicas de regularização e serão assunto do próximo capítulo.
Até lá!
Referências:
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition
Gradient Descent For Machine Learning
Pattern Recognition and Machine Learning

