Capítulo 49 – A Matemática do Backpropagation Through Time (BPTT)
Estudamos no capítulo anterior as Redes Neurais Recorrentes. Mas para que elas funcionem, o algoritmo de treinamento precisa de um pequeno ajuste, uma vez que esse tipo de rede possui o que podemos chamar de “memória” durante seu treinamento. E o que faz isso acontecer é A Matemática do Backpropagation Through Time (BPTT), assunto deste capítulo do Deep Learning Book.
Um Pouco Mais Sobre as RNNs
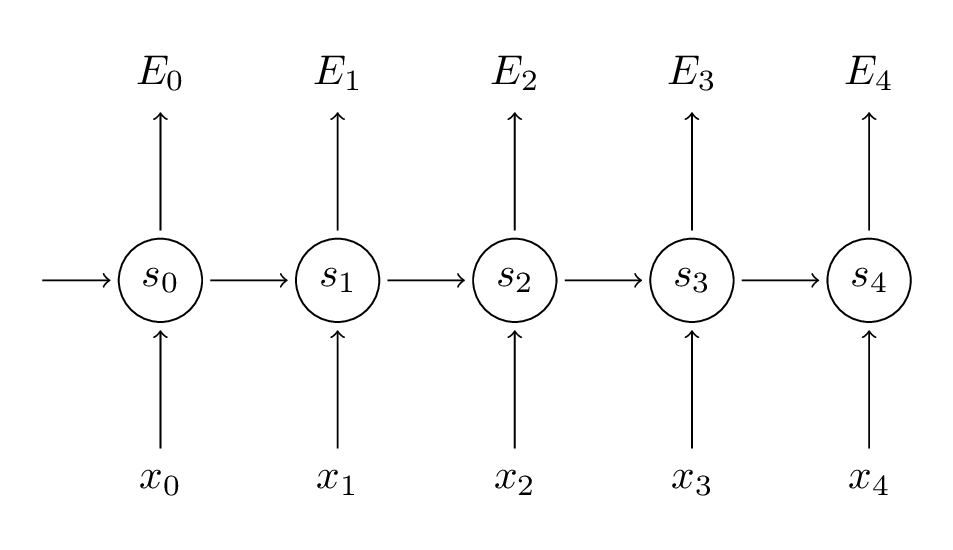
A ideia por trás dos RNNs é fazer uso de informações sequenciais. Em uma rede neural tradicional, assumimos que todas as entradas (e saídas) são independentes umas das outras. Mas para muitas tarefas isso é uma ideia muito ruim. Se você quiser prever a próxima palavra em uma frase, é melhor saber quais palavras vieram antes dela. As RNNs são chamadas de recorrentes porque executam a mesma tarefa para todos os elementos de uma sequência, com a saída sendo dependente dos cálculos anteriores. Outra maneira de pensar sobre RNNs é que elas têm uma “memória” que captura informações sobre o que foi calculado até agora. Em teoria, RNNs podem fazer uso de informações em sequências arbitrariamente longas, mas, na prática, limitam-se a olhar para trás apenas alguns passos (mais sobre isso adiante). Aqui está o que uma RNN típica parece:
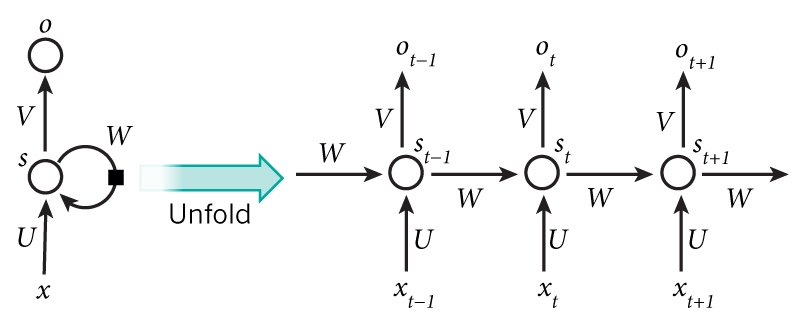
O diagrama acima mostra uma RNN sendo “desenrolada” ou “desdobrada” (termo unfolded em inglês) em uma rede completa. Ao desenrolar, simplesmente queremos dizer que escrevemos a rede para a sequência completa. Por exemplo, se a sequência que nos interessa é uma sentença de 5 palavras, a rede seria desdobrada em uma rede neural de 5 camadas, uma camada para cada palavra. As fórmulas que governam o cálculo que acontece em uma RNN são as seguintes:
1. xt é a entrada no passo de tempo t. Por exemplo, x1 poderia ser um vetor one-hot correspondente à segunda palavra de uma sentença.
2. st é o estado oculto no passo de tempo t. É a “memória” da rede. O termo st é calculado com base no estado oculto anterior e a entrada na etapa atual através da fórmula: st = f(Uxt + Wst-1). A função geralmente é uma não-linearidade, como tanh ou ReLU. Já s -1, que é necessário para calcular o primeiro estado oculto, é tipicamente inicializado com zero.
3. ot é a saída na etapa t. Por exemplo, se quiséssemos prever a próxima palavra em uma frase, seria um vetor de probabilidades em todo o nosso vocabulário. ot = softmax(Vst).
Há algumas coisas a serem observadas aqui:
Você pode pensar no estado oculto st como a memória da rede. st captura informações sobre o que aconteceu em todas as etapas de tempo anteriores. A saída na etapa ot é calculada exclusivamente com base na memória no tempo t. É um pouco mais complicado na prática, porque normalmente não é possível capturar informações de muitas etapas de tempo anteriores.
Ao contrário de uma rede neural profunda tradicional, que usa parâmetros diferentes em cada camada, uma RNN compartilha os mesmos parâmetros (U, V, W acima) em todas as etapas. Isso reflete o fato de que estamos executando a mesma tarefa em cada etapa, apenas com entradas diferentes. Isso reduz muito o número total de parâmetros que precisamos aprender.
O diagrama acima tem saídas em cada etapa de tempo, mas dependendo da tarefa, isso pode não ser necessário. Por exemplo, ao prever o sentimento de uma frase, podemos nos preocupar apenas com a saída final, não com o sentimento após cada palavra. Da mesma forma, podemos não precisar de entradas em cada etapa de tempo. A principal característica de uma RNN é seu estado oculto, que captura algumas informações sobre uma sequência.
E o Backpropagation?
Lembre-se, o objetivo das redes neurais recorrentes é classificar com precisão uma entrada sequencial (por exemplo, dada uma frase, prever o sentimento ou mesmo a próxima palavra). Contamos com a retropropagação (backpropagation) do erro e o gradiente descendente para fazê-lo.
A retropropagação em redes feedforward retrocede do erro final através das saídas, pesos e entradas de cada camada oculta, atribuindo a esses pesos a responsabilidade por uma parte do erro calculando suas derivadas parciais – ∂E / ∂w, ou a relação entre suas taxas de mudança. Essas derivações são então usadas por nossa regra de aprendizado, gradiente descendente, para ajustar os pesos para cima ou para baixo, qualquer que seja a direção que diminua o erro. Já estudamos isso nos capítulos anteriores aqui do Deep Learning Book.
As redes recorrentes dependem de uma extensão da retropropagação, chamada Backpropagation Through Time, ou BPTT. O tempo, neste caso, é simplesmente expresso por uma série ordenada e bem definida de cálculos, ligando um passo de tempo ao seguinte, o que significa que toda a retropropagação precisa funcionar.
Redes neurais, sejam elas recorrentes ou não, são simplesmente funções compostas aninhadas como f(g(h(x))). A adição de um elemento de tempo apenas estende a série de funções para as quais calculamos derivadas com a regra da cadeia (chain rule). Matemática pura!
A Matemática do Backpropagation Through Time (BPTT)
Por falar em Matemática, vamos compreender o BPTT através de fórmulas e alguns gráficos. Para as devidas referências, sempre consulte as notas ao final do capítulo.
Considere que estamos criando uma rede neural recorrente que seja capaz de prever a próxima palavra em um texto, o que pode ser útil em aplicações de IA para criar petições e assim ajudar advogados a automatizar o trabalho. Algo que já é feito pelo ROSS, o Robô Advogado.
Vamos começar com a equação básica de uma Rede Neural Recorrente:
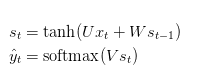
Também definimos nossa perda, ou erro, como a perda de entropia cruzada, dada por:
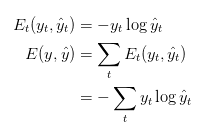
Aqui, yt é a palavra correta no momento do passo t, e y^t é nossa previsão. Normalmente, tratamos a sequência completa (sentença) como um exemplo de treinamento, portanto, o erro total é apenas a soma dos erros em cada etapa de tempo (palavra).
Lembre-se de que nosso objetivo é calcular os gradientes do erro em relação aos nossos parâmetros U, V e W e, em seguida, aprender bons parâmetros usando o Gradiente Descendente Estocástico. Assim como resumimos os erros, também somamos os gradientes em cada etapa de tempo para um exemplo de treinamento:
![]()
Para calcular esses gradientes, usamos a regra de diferenciação da cadeia. Esse é o algoritmo de retropropagação quando aplicado para trás a partir do erro. Usaremos o E_3 como exemplo, apenas para trabalhar com números concretos.
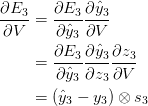
Acima, z3 = Vs3 e a última linha é o produto externo de dois vetores. Não se preocupe se você não seguir os passos acima, nós pulamos vários passos e você pode tentar calcular essas derivadas você mesmo (bom exercício!). O ponto que estou tentando transmitir é que
![]()
depende apenas dos valores no momento atual, yˆ3, y3, s3. Se você tem estes valores, calculando o gradiente para V é uma multiplicação de matriz simples. Mas a história é diferente para W (e para U):
![]()
Para entender porque, escrevemos a regra da cadeia, como acima:
![]()
Agora, note que s3 = tanh(Uxt + Ws2) depende de s2, que depende de W e s1, e assim por diante. Então, se pegarmos a derivada em relação a W, não podemos simplesmente tratar s2 como uma constante! Precisamos aplicar a regra da cadeia novamente e o que realmente temos é o seguinte:
![]()
Somamos as contribuições de cada passo de tempo para o gradiente. Em outras palavras, como W é usado em todas as etapas até a saída que nos interessa, precisamos retroceder gradientes na rede de t = 3 até t = 0:
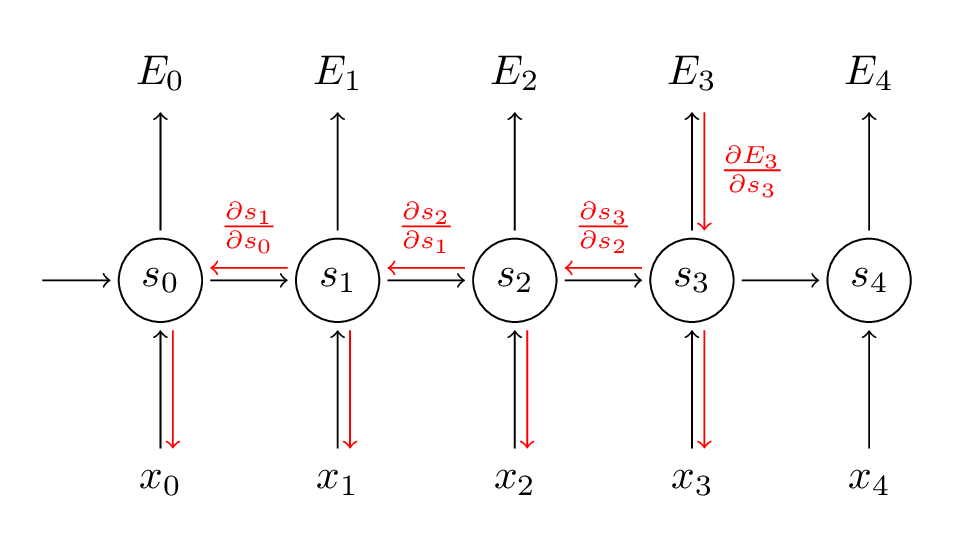
Observe que isso é exatamente o mesmo que o algoritmo de retropropagação padrão que usamos nas Redes Neurais Profundas da Feedforward. A principal diferença é que resumimos os gradientes para W em cada etapa de tempo. Em um rede neural tradicional, não compartilhamos parâmetros entre camadas, portanto, não precisamos somar nada. Mas, na minha opinião, o BPTT é apenas um nome sofisticado para retropropagação padrão em uma RNN “desenrolada”. Assim como com Backpropagation, você pode definir um vetor delta que você repassa, por exemplo:
![]()
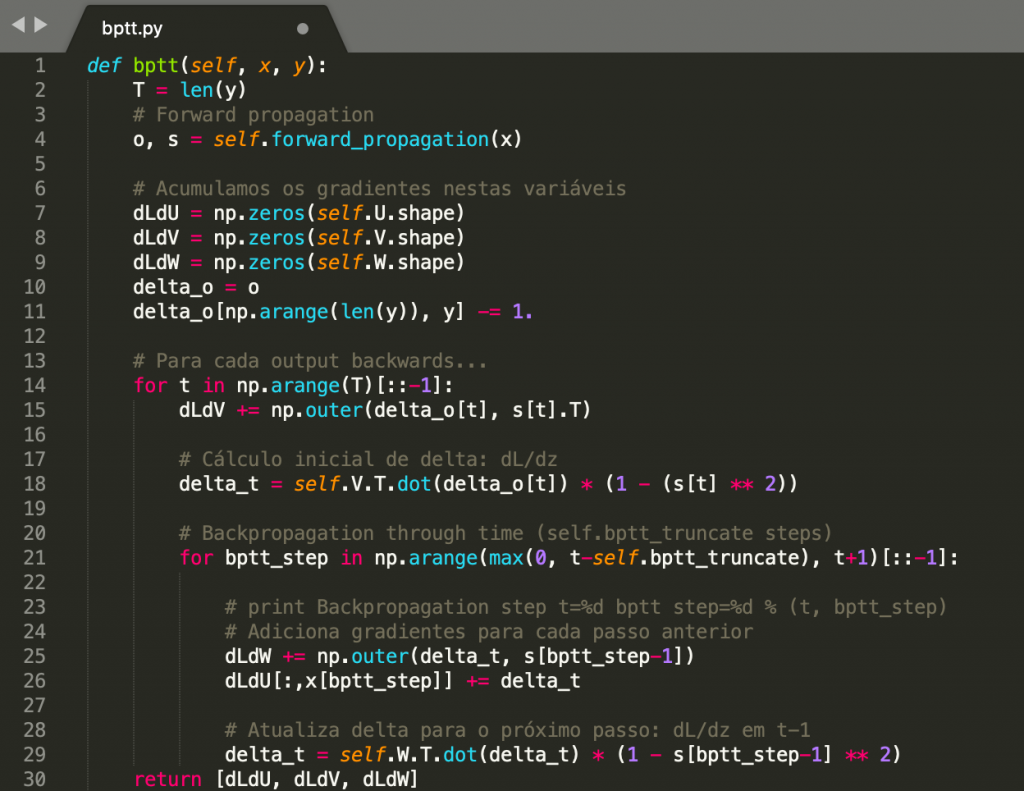
Aqui um exemplo de como seria a implementação do BPTT em Python:
Isso também deve lhe dar uma ideia do motivo pelo qual as RNNs são difíceis de treinar: as sequências (frases) podem ser bastante longas, talvez 20 palavras ou mais, e, portanto, você precisa retroceder através de várias camadas. Na prática, muitas pessoas truncam a retropropagação em poucos passos. Mas isso é assunto para o próximo capítulo! Até lá.
Referências:
Recurrent Neural Networks Cheatsheet
A Beginner’s Guide to LSTMs and Recurrent Neural Networks
Recurrent Neural Networks Tutorial, Part 1 – Introduction to RNNs
Recurrent Neural Networks Tutorial, Part 3 – Backpropagation Through Time and Vanishing Gradients
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition
Gradient Descent For Machine Learning
Pattern Recognition and Machine Learning