Capítulo 57 – Os Detalhes Matemáticos das GANs (Generative Adversarial Networks)

Neste capítulo vamos concluir nosso estudo das GANs com os detalhes matemáticos, antes de avançar para outra arquitetura de Deep Learning que estudaremos na sequência. Estamos considerando que você leu os capítulos anteriores sobre GANs.

A modelagem de redes neurais requer essencialmente definir duas coisas: uma arquitetura e uma função de perda. Já descrevemos a arquitetura de redes adversárias generativas. Consiste em duas redes:

Uma rede generativa G que recebe uma entrada aleatória z com densidade p_z e retorna uma saída x_g = G (z) que deve seguir (após o treinamento) a distribuição de probabilidade alvo.
Uma rede discriminativa D que recebe uma entrada x que pode ser uma entrada “verdadeira” (x_t, cuja densidade é denotada p_t) ou uma entrada “gerada” (x_g, cuja densidade p_g é a densidade induzida pela densidade p_z através de G) e que retorna a probabilidade D (x) de x para ser um dado “verdadeiro”.

Vamos agora examinar mais de perto a função de perda “teórica” das GANs. Se enviarmos ao discriminador dados “verdadeiros” e “gerados” nas mesmas proporções, o erro absoluto esperado do discriminador poderá ser expresso como:

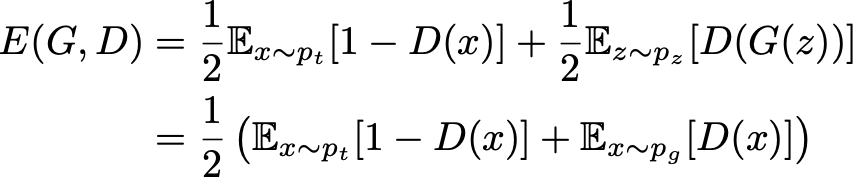
O objetivo do gerador é enganar o discriminador cujo objetivo é ser capaz de distinguir entre dados verdadeiros e dados gerados. Portanto, ao treinar o gerador, queremos maximizar esse erro enquanto tentamos minimizá-lo para o discriminador. Isso nos dá a fórmula abaixo:

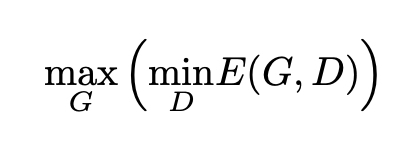
Para qualquer gerador G (juntamente com a densidade de probabilidade induzida p_g), o melhor discriminador possível é aquele que minimiza a integral abaixo:

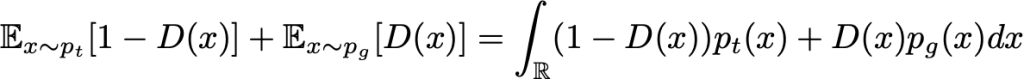
Para minimizar (em relação a D) essa integral, podemos minimizar a função dentro da integral para cada valor de x. Em seguida, definimos o melhor discriminador possível para um determinado gerador:

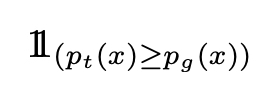
(de fato, um dos melhores porque x valores tais que p_t (x) = p_g (x) podem ser manipulados de outra maneira, mas isso não importa para o que segue). Em seguida, pesquisamos G que maximiza:

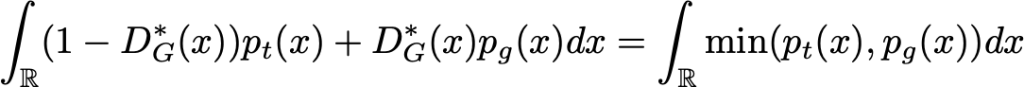
Parece complexo? É menos do que parece e explicamos sobre os fundamentos matemáticos por trás dessas fórmulas no curso Matemática Para Data Science. Novamente, para maximizar (em relação a G) essa integral, podemos maximizar a função dentro da integral para cada valor de x. Como a densidade p_t é independente do gerador G, não podemos fazer melhor do que definir G de modo que:

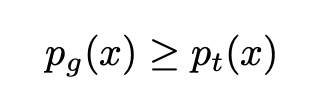
Obviamente, como p_g é uma densidade de probabilidade que deve se integrar a 1, necessariamente temos o melhor G:

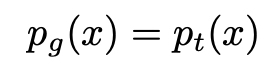
Assim, mostramos que, em um caso ideal com gerador e discriminador de capacidade ilimitada, o ponto ideal do cenário adversário é tal que o gerador produz a mesma densidade que a densidade real e o discriminador não pode fazer melhor do que ser verdadeiro em um caso a cada dois, exatamente como a intuição nos disse. Por fim, observe também que G maximiza:

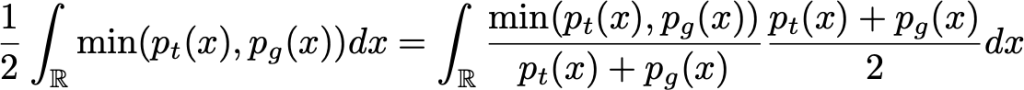
Na fórmula acima vemos que G deseja maximizar a probabilidade esperada de o discriminador estar errado.

Conclusão Sobre as GANs

As GANs são bem recentes e possuem uma ideia inovadora sobre como treinar uma arquitetura de rede neural. Muitos estudos e aplicações vem sendo feitos em todo mundo e já existem até algumas aplicações comerciais usando essa arquitetura de Deep Learning. Caso queira aprender a construir GANs na prática, acesse aqui.

Pontos mais importantes sobre as GANs:

Computadores podem basicamente gerar variáveis pseudo-aleatórias simples (por exemplo, eles podem gerar variáveis que seguem muito de perto uma distribuição uniforme).
Existem maneiras diferentes de gerar variáveis aleatórias mais complexas, incluindo a noção de “método de transformação” que consiste em expressar uma variável aleatória em função de algumas variáveis aleatórias mais simples.
No aprendizado de máquina, os modelos generativos tentam gerar dados de uma determinada distribuição de probabilidade (complexa). Modelos generativos de aprendizado profundo são modelados como redes neurais (funções muito complexas) que recebem como entrada uma variável aleatória simples e retornam uma variável aleatória que segue a distribuição direcionada (como “método de transformação”).
Essas redes generativas podem ser treinadas “diretamente” (comparando a distribuição dos dados gerados com a verdadeira distribuição): esta é a ideia das redes correspondentes generativas
Essas redes generativas também podem ser treinadas “indiretamente” (tentando enganar outra rede treinada ao mesmo tempo para distinguir dados “gerados” de dados “verdadeiros”): essa é a ideia das redes adversas generativas.
Mesmo que o “hype” que rodeia os GANs seja talvez um pouco exagerado, podemos dizer que a ideia de treinamento antagônico sugerida por Ian Goodfellow e seus co-autores é realmente ótima. Essa maneira de distorcer a função de perda, passando de uma comparação direta para uma indireta, é realmente algo que pode ser muito inspirador para futuros trabalhos na área de aprendizado profundo.

Referências:

Análise Estatística Para Data Science com Linguagem Python

Customizando Redes Neurais com Funções de Ativação Alternativas

A Beginner’s Guide to Generative Adversarial Networks (GANs)

A Leap into the Future: Generative Adversarial Networks

Understanding Generative Adversarial Networks (GANs)

How A.I. Is Creating Building Blocks to Reshape Music and Art

Train longer, generalize better: closing the generalization gap in large batch training of neural networks

Practical Recommendations for Gradient-Based Training of Deep Architectures

Gradient-Based Learning Applied to Document Recognition

Neural Networks & The Backpropagation Algorithm, Explained

Neural Networks and Deep Learning