Capítulo 61 – A Matemática dos Variational Autoencoders (VAEs)
No capítulo anterior, fornecemos a seguinte visão geral intuitiva: Os VAEs são Autoencoders que codificam entradas como distribuições em vez de pontos e cuja “organização” do espaço latente é regularizada restringindo as distribuições retornadas pelo codificador a estarem próximas de um gaussiano padrão. Neste capítulo, forneceremos uma visão matemática dos VAEs que nos permitirá justificar o termo de regularização com mais rigor. Para isso, definiremos uma estrutura probabilística clara e usaremos, em particular, a técnica de inferência variacional.
Estrutura Probabilística e Premissas
Vamos começar definindo um modelo gráfico probabilístico para descrever nossos dados. Denotamos por x a variável que representa nossos dados e assumimos que x é gerado a partir de uma variável latente z (a representação codificada) que não é diretamente observada. Assim, para cada ponto de dados, é assumido o seguinte processo generativo de duas etapas:
- Primeiro, uma representação latente z é amostrada da distribuição anterior p(z).
- Segundo, os dados x são amostrados da distribuição de probabilidade condicional definido por p(x | z).
Com esse modelo probabilístico em mente, podemos redefinir nossas noções de codificador e decodificador. De fato, ao contrário de um Autoencoder simples que considera codificador e decodificador determinístico, consideraremos agora versões probabilísticas desses dois objetos. O “decodificador probabilístico” é definido naturalmente por p(x | z), que descreve a distribuição da variável decodificada dada a codificada, enquanto o “codificador probabilístico” é definido por p(z | x), que descreve a distribuição de a variável codificada, dada a decodificada.
Neste ponto, já podemos notar que a regularização do espaço latente que nos faltava em Autoencoders simples aparece naturalmente aqui na definição do processo de geração de dados: presume-se que representações codificadas z no espaço latente sigam a distribuição anterior p(z). Caso contrário, também podemos lembrar o conhecido teorema de Bayes, que faz a ligação entre o anterior p(z), a probabilidade p(x | z) e o posterior p(z | x):
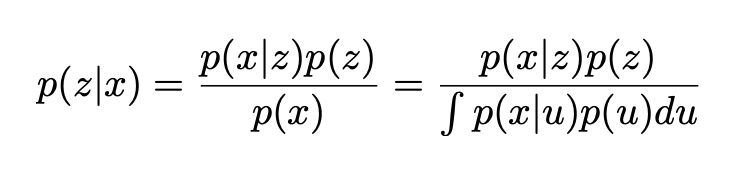
Vamos agora assumir que p(z) é uma distribuição gaussiana padrão e que p(x | z) é uma distribuição gaussiana cuja média é definida por uma função determinística f da variável de z e cuja matriz de covariância tem a forma de uma constante positiva c que multiplica a matriz de identidade I. Supõe-se que a função f pertence a uma família de funções denotadas F que é deixada não especificada no momento e que será escolhida posteriormente. Assim, temos:
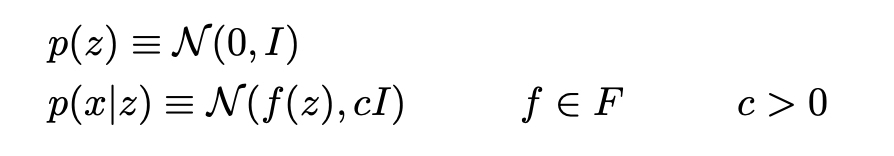
Vamos considerar, por enquanto, que f está bem definido e fixo. Em teoria, como conhecemos p(z) e p(x | z), podemos usar o Teorema de Bayes para calcular p(z | x): este é um problema clássico de inferência bayesiana. No entanto, esse tipo de computação geralmente é intratável (por causa da integral no denominador) e requer o uso de técnicas de aproximação, como inferência variacional.
Nota: Aqui podemos mencionar que p(z) e p(x | z) são ambas distribuições gaussianas, implicando que p(z | x) também deve seguir uma distribuição gaussiana. Em teoria, poderíamos “apenas” tentar expressar a média e a matriz de covariância de p(z | x) com relação às médias e às matrizes de covariância de p(z) e p(x | z). No entanto, na prática, esses valores dependem da função f que pode ser complexa e que não está definida por enquanto (mesmo que tenhamos assumido o contrário). Além disso, o uso de uma técnica de aproximação como inferência variacional torna a abordagem bastante geral e mais robusta a algumas mudanças na hipótese do modelo.
Formulação de Inferência Variacional
Em Estatística, a inferência variacional é uma técnica para aproximar distribuições complexas. A ideia é definir uma família de distribuição parametrizada (por exemplo, a família de Gaussianos, cujos parâmetros são a média e a covariância) e procurar a melhor aproximação de nossa distribuição de destino entre essa família. O melhor elemento da família é aquele que minimiza uma determinada medição de erro de aproximação (na maioria das vezes a divergência de Kullback-Leibler entre aproximação e alvo) e é encontrada por descida do gradiente sobre os parâmetros que descrevem a família. Para mais detalhes, você encontra um artigo sobe isso na seção de referências ao final do capítulo.
Aqui vamos aproximar p(z | x) por uma distribuição gaussiana q_x(z) cuja média e covariância são definidas por duas funções, g e h, do parâmetro x. Essas duas funções devem pertencer, respectivamente, às famílias de funções G e H que serão especificadas mais tarde, mas que devem ser parametrizadas. Assim, podemos denotar:
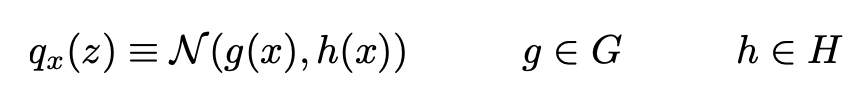
Portanto, definimos dessa maneira uma família de candidatos à inferência variacional e precisamos agora encontrar a melhor aproximação entre essa família otimizando as funções g e h (de fato, seus parâmetros) para minimizar a divergência de Kullback-Leibler entre a aproximação e o alvo p(z | x). Em outras palavras, estamos procurando a aproximação ideal g* e h* de modo que:
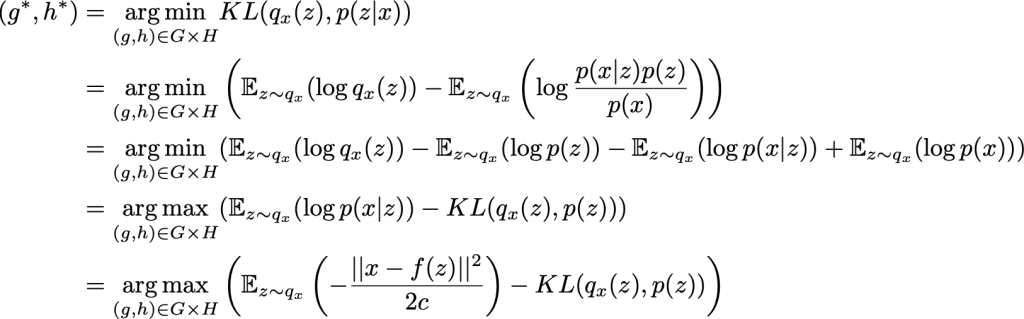
Na penúltima equação, podemos observar a troca existente – ao aproximar-se do p(z | x) posterior – entre maximizar a probabilidade das “observações” (maximização da probabilidade logarítmica esperada para o primeiro termo) e permanecer próximo à distribuição anterior (minimização da divergência de KL entre q_x(z) e p(z), para o segundo termo). Essa troca é natural para o problema de inferência bayesiana e expressa o equilíbrio que precisa ser encontrado entre a confiança que temos nos dados e a confiança que temos no passado.
Até agora, assumimos a função f conhecida e fixa e mostramos que, com tais premissas, podemos aproximar o p(z | x) posterior usando a técnica de inferência variacional. No entanto, na prática, essa função f, que define o decodificador, não é conhecida e também precisa ser escolhida. Para fazer isso, lembre-se de que nosso objetivo inicial é encontrar um esquema de codificação e decodificação com desempenho, cujo espaço latente seja regular o suficiente para ser usado para fins generativos. Se a regularidade é regida principalmente pela distribuição anterior assumida no espaço latente, o desempenho do esquema geral de codificação / decodificação depende muito da escolha da função f.
De fato, como p(z | x) pode ser aproximado (por inferência variacional) de p(z) e p(x | z) e como p(z) é um gaussiano padrão simples, as duas únicas alavancas que temos à nossa disposição em nosso modelo para fazer otimizações são o parâmetro c (que define a variância da probabilidade) e a função f (que define a média da probabilidade).
Portanto, vamos considerar que, como discutimos anteriormente, podemos obter para qualquer função f em F (cada uma definindo um decodificador probabilístico diferente p(x | z)) a melhor aproximação de p(z | x), denotada q*_x(z) Apesar de sua natureza probabilística, estamos procurando um esquema de codificação-decodificação o mais eficiente possível e, em seguida, queremos escolher a função f que maximize a probabilidade logarítmica esperada de x dado z quando z é amostrado de q*_x(z) Em outras palavras, para uma dada entrada x, queremos maximizar a probabilidade de ter x̂ = x quando amostramos z da distribuição q*_x(z) e depois amostramos x̂ da distribuição p(x | z). Assim, procuramos o f* ideal para que:
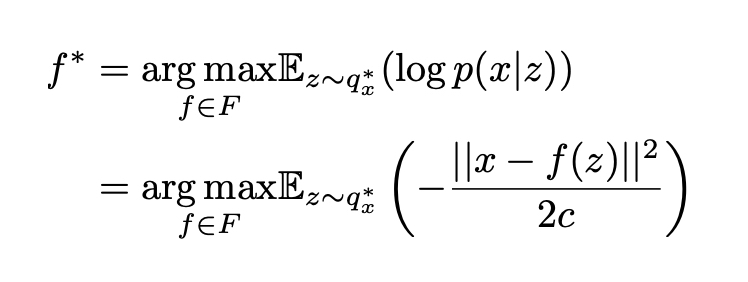
onde q*_x (z) depende da função f e é obtido como descrito anteriormente. Reunindo todas as peças, estamos procurando as aproximações f*, g* e h* ideais para que:
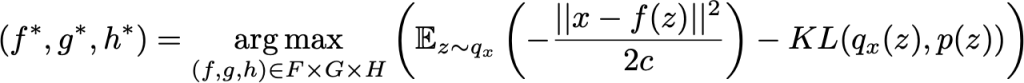
Podemos identificar nesta função objetivo os elementos introduzidos na descrição intuitiva dos VAEs dados no capítulo anterior: o erro de reconstrução entre x e f(z) e o termo de regularização dado pela divergência KL entre q_x(z) e p(z) ) (que é um gaussiano padrão). Também podemos notar a constante c que regula o equilíbrio entre os dois termos anteriores. Quanto maior c for, mais assumimos uma alta variação em torno de f(z) para o decodificador probabilístico em nosso modelo e, portanto, mais favorecemos o termo de regularização sobre o termo de reconstrução (e o oposto se c for baixo).
Trazendo Redes Neurais Para o Modelo
Até o momento, definimos um modelo probabilístico que depende de três funções, f, g e h, e expressamos, usando inferência variacional, o problema de otimização a ser resolvido para obter f*, g* e h* que ofereçam o melhor esquema de codificação-decodificação com este modelo. Como não podemos otimizar facilmente todo o espaço de funções, restringimos o domínio de otimização e decidimos expressar f, g e h como redes neurais. Assim, F, G e H correspondem, respectivamente, às famílias de funções definidas pelas arquiteturas de rede e a otimização é feita sobre os parâmetros dessas redes.
Na prática, g e h não são definidos por duas redes completamente independentes, mas compartilham uma parte de sua arquitetura e seus pesos, de modo que temos:
![]()
Como isso define a matriz de covariância de q_x(z), h(x) deve ser uma matriz quadrada. Entretanto, para simplificar o cálculo e reduzir o número de parâmetros, assumimos que nossa aproximação de p(z | x), q_x(z), é uma distribuição gaussiana multidimensional com matriz de covariância diagonal (assunção de independência de variáveis). Com essa suposição, h(x) é simplesmente o vetor dos elementos diagonais da matriz de covariância e, então, tem o mesmo tamanho de g(x). No entanto, reduzimos dessa maneira a família de distribuições que consideramos para inferência variacional e, portanto, a aproximação de p(z | x) obtida pode ser menos precisa.
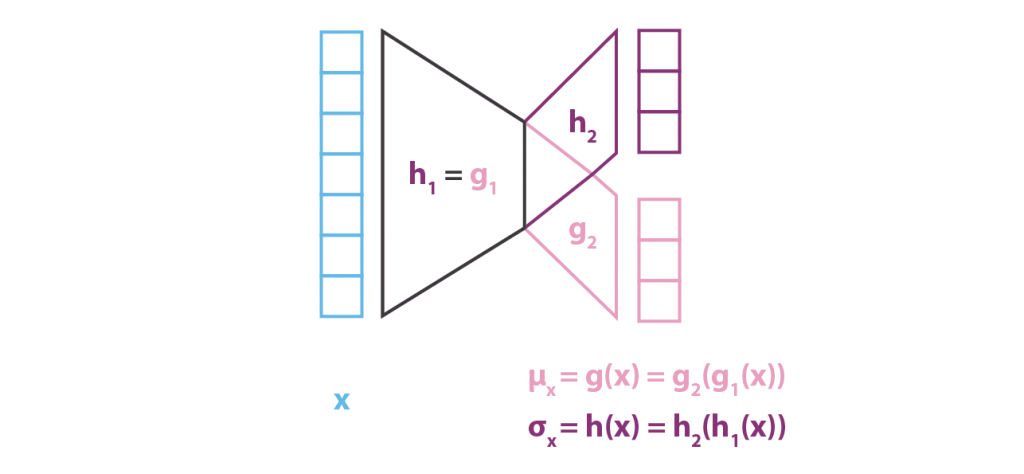
Ao contrário da parte do codificador que modela p(z | x) e para a qual consideramos um gaussiano com média e covariância que são funções de x(g e h), nosso modelo assume para p(x | z) um gaussiano com covariância. A função f da variável z que define a média desse gaussiano é modelada por uma rede neural e pode ser representada da seguinte forma:
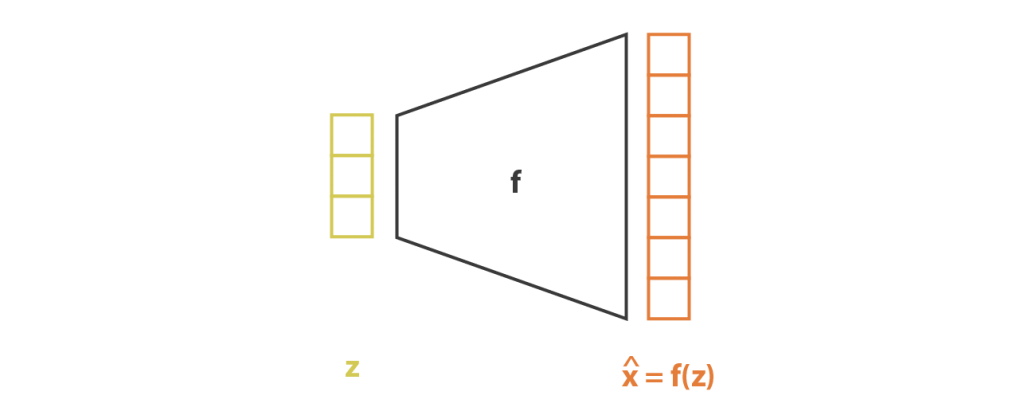
A arquitetura geral é então obtida concatenando o codificador e as partes do decodificador. No entanto, ainda precisamos ter muito cuidado com a maneira como coletamos amostras da distribuição retornada pelo codificador durante o treinamento. O processo de amostragem deve ser expresso de forma a permitir que o erro seja retropropagado pela rede. Um truque simples, chamado truque de reparametrização, é usado para tornar possível a descida do gradiente, apesar da amostragem aleatória que ocorre na metade da arquitetura e consiste em usar o fato de que se z é uma variável aleatória após uma distribuição gaussiana com média g(x) e com covariância h(x), pode ser expresso como:
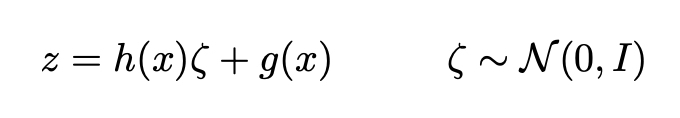
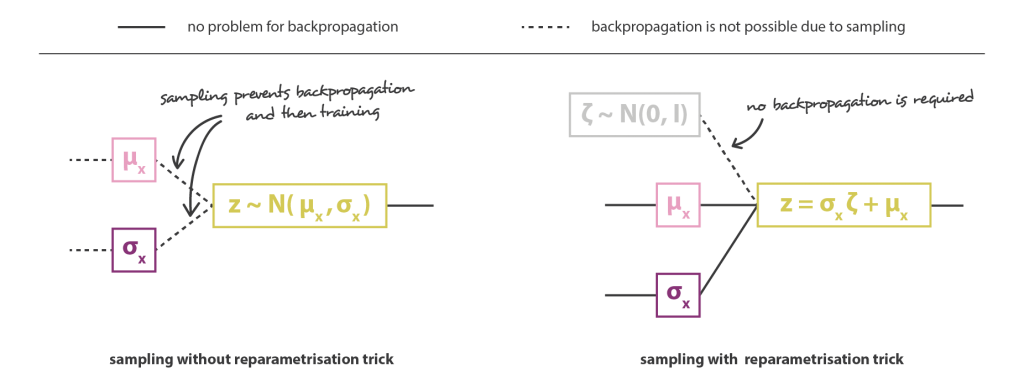
Finalmente, a função objetivo da arquitetura de Autoencoder Variacional obtida dessa maneira é dada pela última equação da subseção anterior, na qual a expectativa teórica é substituída por uma aproximação de Monte-Carlo mais ou menos precisa que consiste, na maioria das vezes, em um sorteio único. Assim, considerando essa aproximação e denotando C = 1 / (2c), recuperamos a função de perda derivada intuitivamente na seção anterior, composta por um termo de reconstrução, um termo de regularização e uma constante para definir os pesos relativos desses dois termos.
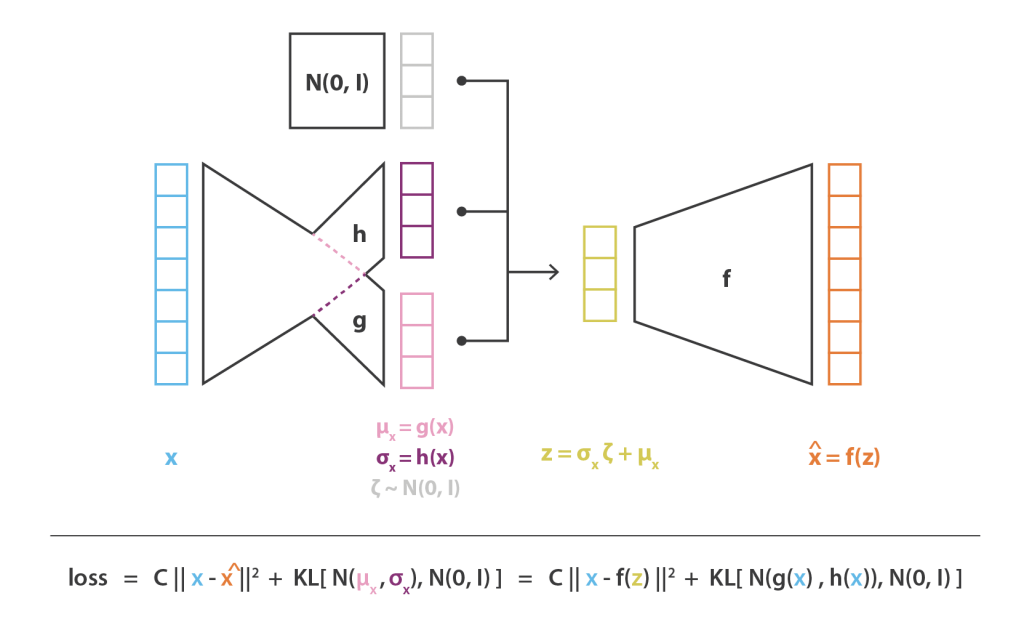
Autoencoders Variacionais (VAEs) são Autoencoders que resolvem o problema da irregularidade do espaço latente, fazendo com que o codificador retorne uma distribuição sobre o espaço latente em vez de um único ponto e adicionando à função de perda um termo de regularização sobre a distribuição retornada para garantir uma melhor organização do espaço latente assumindo um modelo probabilístico simples para descrever nossos dados, a função de perda bastante intuitiva dos VAEs, composta por um termo de reconstrução e um termo de regularização, pode ser cuidadosamente derivada, usando em particular a técnica estatística de inferência variacional (daí o nome Autoencoder “Variacional”).
Para concluir, podemos destacar que, durante os últimos anos, as GANs se beneficiaram de muito mais contribuições científicas do que os VAEs. Entre outras razões, o maior interesse demonstrado pela comunidade por GANs pode ser parcialmente explicado pelo maior grau de complexidade na base teórica dos VAEs (modelo probabilístico e inferência variacional) em comparação à simplicidade do conceito de treinamento adversário que rege os GANs. Com este capítulo, esperamos que tenhamos compartilhado intuições valiosas e fortes fundamentos teóricos para tornar os VAEs mais acessíveis aos recém-chegados. No entanto, agora que discutimos em profundidade os dois, resta uma pergunta … qual arquitetura você achou mais interessante, GANs ou VAEs?
No próximo capítulo começamos a estudar a Aprendizagem Por Reforço! Até lá.
Referências:
Customizando Redes Neurais com Funções de Ativação Alternativas
Autoencoders – Unsupervised Learning
Bayesian inference problem, MCMC and variational inference
Understanding Variational Autoencoders (VAEs)
Deep Learning — Different Types of Autoencoders
Contractive Auto-Encoders – Explicit Invariance During Feature Extraction
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Recurrent neural network based language model
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

