Capítulo 31 – As Redes Neurais Artificiais Podem Computar Qualquer Função?
Um dos fatos mais impressionantes sobre redes neurais é que elas podem computar qualquer função. Isto é, suponha que alguém lhe dê alguma função complicada, f(x):
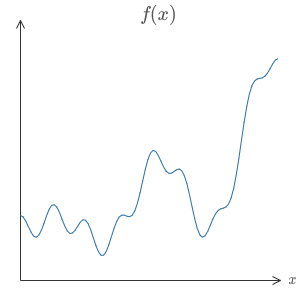
Não importa qual seja a função, é garantido que existe uma rede neural de modo que, para cada entrada possível, x, o valor f(x) (ou alguma aproximação) seja transmitido da rede, por exemplo:
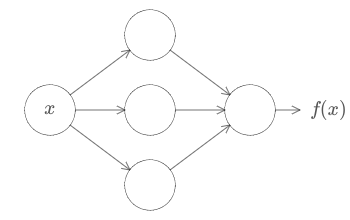
Este resultado é válido mesmo se a função tiver muitas entradas, f = f(x1,…, xm) e muitas saídas. Por exemplo, aqui está uma rede computando uma função com m = 3 entradas e n = 2 saídas:
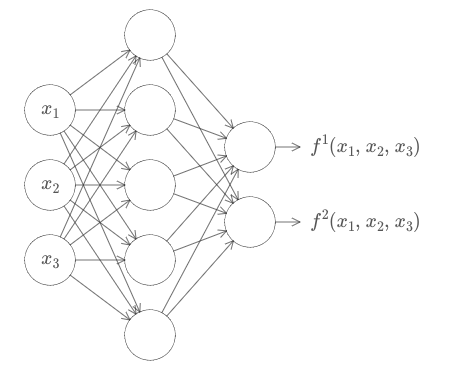
Este resultado nos diz que as redes neurais têm um tipo de universalidade. Não importa qual função queremos computar, sabemos que existe uma rede neural que pode fazer o trabalho.
Além do mais, esse teorema da universalidade é válido mesmo se restringirmos nossas redes a ter apenas uma única camada intermediária entre os neurônios de entrada e de saída – uma chamada camada oculta única. Portanto, mesmo arquiteturas de rede muito simples podem ser extremamente poderosas e isso ajuda a explicar porque as redes neurais vem sendo usadas em aplicações avançadas de Inteligência Artificial.
O teorema da universalidade é bem conhecido por pessoas que usam redes neurais. Mas porque é verdade não é tão amplamente compreendido. A maioria das explicações disponíveis é bastante técnica. Por exemplo, um dos artigos originais que comprovou o resultado utilizou o teorema de Hahn-Banach, o teorema da representação de Riesz e alguma análise de Fourier. Se você é um matemático, o argumento não é difícil de seguir, mas não é tão fácil para a maioria das pessoas. É uma pena, já que as razões subjacentes à universalidade são simples e belas.
Nos próximos capítulos, faremos uma explicação simples e principalmente visual do teorema da universalidade. Nós vamos passo a passo através das idéias principais. Você entenderá porque é verdade que as redes neurais podem computar qualquer função. Você entenderá algumas das limitações do resultado. E você entenderá como o resultado se relaciona com redes neurais profundas (Deep Learning).
Os capítulos serão estruturados para ser agradáveis e objetivos. Desde que você tenha apenas um pouco de familiaridade básica com redes neurais, você deve ser capaz de seguir a explicação. No entanto, iremos fornecer links ocasionais para materiais anteriores, para ajudar a preencher quaisquer lacunas em seu conhecimento.
Os teoremas da universalidade são um lugar comum na ciência da computação, tanto que às vezes nos esquecemos do quão surpreendentes eles são. Mas vale a pena lembrar-nos: a capacidade de calcular uma função arbitrária é verdadeiramente notável. Quase qualquer processo que você possa imaginar pode ser considerado como computação de função. Considere o problema de nomear uma peça musical com base em uma pequena amostra da peça. Isso pode ser pensado como computação de uma função. Ou considere o problema de traduzir um texto chinês para o inglês. Mais uma vez, isso pode ser pensado como computação de uma função. Ou considere o problema de analisar um arquivo de filme mp4 e gerar uma descrição do enredo do filme e uma discussão sobre a qualidade da atuação dos atores. Novamente, isso pode ser pensado como um tipo de computação de função. Universalidade significa que, em princípio, as redes neurais podem fazer tudo isso e muito mais.
É claro, só porque sabemos que existe uma rede neural que pode (por exemplo) traduzir o texto chinês para o inglês, isso não significa que temos boas técnicas para construir ou mesmo reconhecer tal rede. Essa limitação se aplica também aos teoremas da universalidade tradicionais para modelos como circuitos booleanos. Mas, como vimos anteriormente no livro, as redes neurais possuem algoritmos poderosos para funções de aprendizado. Essa combinação de algoritmos de aprendizado + universalidade é uma mistura atraente. Até agora, o livro se concentrou nos algoritmos de aprendizado. Nos próximos capítulos, nos concentramos na universalidade e no que ela significa.
A compreensão desse conceito é a chave para as arquiteturas mais avançadas de Deep Learning, que estão por vir mais a frente, neste livro!
Referências:
Desenvolvimento e Deploy de Modelos de Machine Learning
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

