Capítulo 35 – A Matemática do Problema de Dissipação do Gradiente em Deep Learning
Vamos continuar a discussão iniciada no capítulo anterior. Para entender porque o problema da dissipação do gradiente ocorre, vamos considerar a rede neural profunda mais simples: uma com apenas um único neurônio em cada camada. Aqui está uma rede com três camadas ocultas:
![]()
Aqui, w1, w2,… são os pesos, b1, b2,… são os vieses e C é alguma função de custo. Apenas para lembrar como isso funciona, a saída aj do neurônio j é σ(zj), onde σ é a função de ativação sigmóide usual, e zj = wjaj − 1 + bj é a entrada ponderada para o neurônio. Eu desenhei o custo C no final para enfatizar que o custo é uma função da saída da rede, a4: se a saída real da rede estiver próxima da saída desejada, então o custo será baixo, enquanto se estiver longe, o custo será alto.
Vamos estudar o gradiente ∂C / ∂b1 associado ao primeiro neurônio oculto. Definiremos uma expressão para ∂C / ∂b1 e, estudando essa expressão, entenderemos porque o problema da dissipação do gradiente ocorre.
Vou começar simplesmente mostrando a expressão para ∂C / ∂b1. Parece assustador, mas na verdade tem uma estrutura simples, que descreverei em breve. Aqui está a expressão (ignore a rede, por enquanto, e note que σ ′ é apenas a derivada da função σ):

A estrutura na expressão é a seguinte: existe um termo σ ′ (zj) no produto para cada neurônio na rede; um peso wj para cada peso na rede; e um termo final ∂C / ∂a4, correspondente à função de custo no final. Observe que coloquei cada termo na expressão acima da parte correspondente da rede. Então a rede em si é um mnemônico para a expressão.
Há também uma explicação simples de porque a expressão acima é verdadeira e, portanto, é divertido (e talvez esclarecedor) dar uma olhada nessa explicação.
Imagine que fazemos uma pequena mudança Δb1 no viés b1. Isso irá desencadear uma série de mudanças em cascata no resto da rede. Primeiro, causa uma mudança Δa1 na saída do primeiro neurônio oculto. Isso, por sua vez, causará uma mudança Δz2 na entrada ponderada para o segundo neurônio oculto. Então, uma mudança Δa2 na saída do segundo neurônio oculto. E assim por diante, até chegar a uma mudança de C no custo na saída. Nós temos
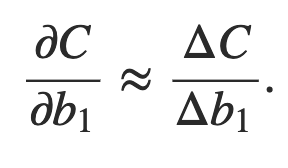
Isso sugere que podemos descobrir uma expressão para o gradiente ∂C / ∂b1, acompanhando cuidadosamente o efeito de cada etapa dessa cascata.
Para fazer isso, vamos pensar em como Δb1 faz com que a saída a1 do primeiro neurônio oculto mude. Nós temos a1 = σ (z1) = σ (w1a0 + b1), então:
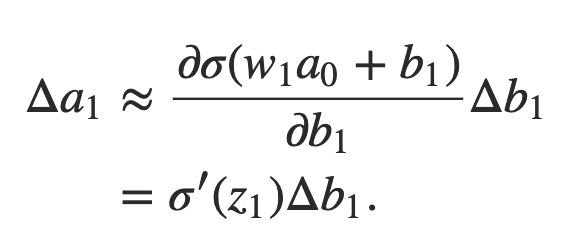
Esse termo σ ′ (z1) deve parecer familiar: é o primeiro termo em nossa expressão reivindicada para o gradiente ∂C / ∂b1. Intuitivamente, esse termo converte uma mudança Δb1 no viés em uma mudança Δa1 na ativação de saída. Essa mudança Δa1 por sua vez causa uma mudança na entrada ponderada z2 = w2a1 + b2 para o segundo neurônio oculto:
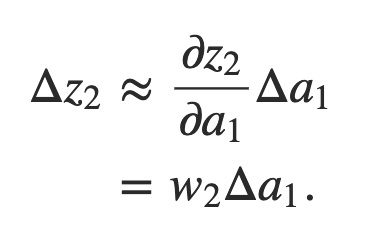
Combinando nossas expressões para Δz2 e Δa1, vemos como a mudança no viés b1 se propaga ao longo da rede para afetar z2:
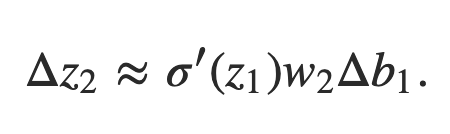
Novamente, isso deve parecer familiar: agora temos os dois primeiros termos em nossa expressão reivindicada para o gradiente ∂C / ∂b1.
Podemos continuar dessa maneira, rastreando a maneira como as alterações se propagam pelo resto da rede. Em cada neurônio, pegamos um termo σ ′ (zj) e, em cada peso, escolhemos um termo wj. O resultado final é uma expressão que relaciona a mudança final ΔC no custo para a mudança inicial Δb1 no viés:
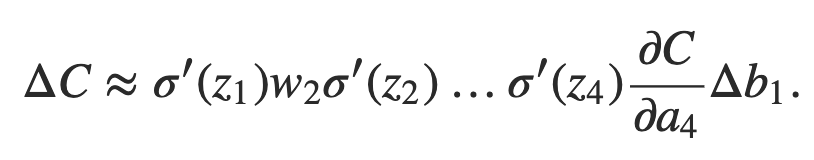
Dividindo por Δb1, de fato, obtemos a expressão desejada para o gradiente:
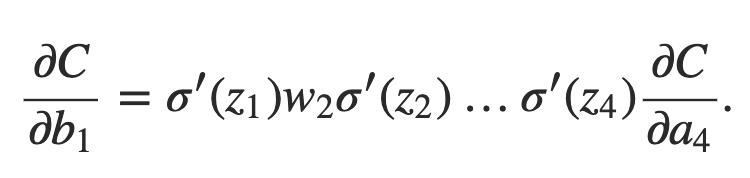
Por que o problema da dissipação do gradiente ocorre afinal?
Para entender porque o problema da dissipação do gradiente ocorre, vamos escrever explicitamente a expressão inteira para o gradiente:
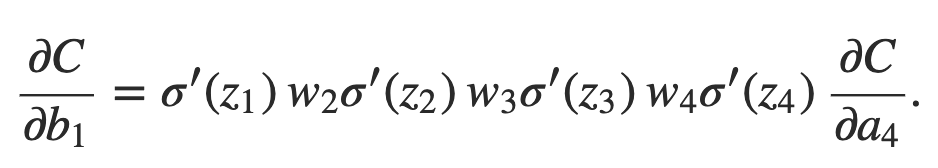
Com exceção do último termo, essa expressão é um produto de termos da forma wjσ ′ (zj). Para entender como cada um desses termos se comporta, vamos ver um gráfico da função σ ′:
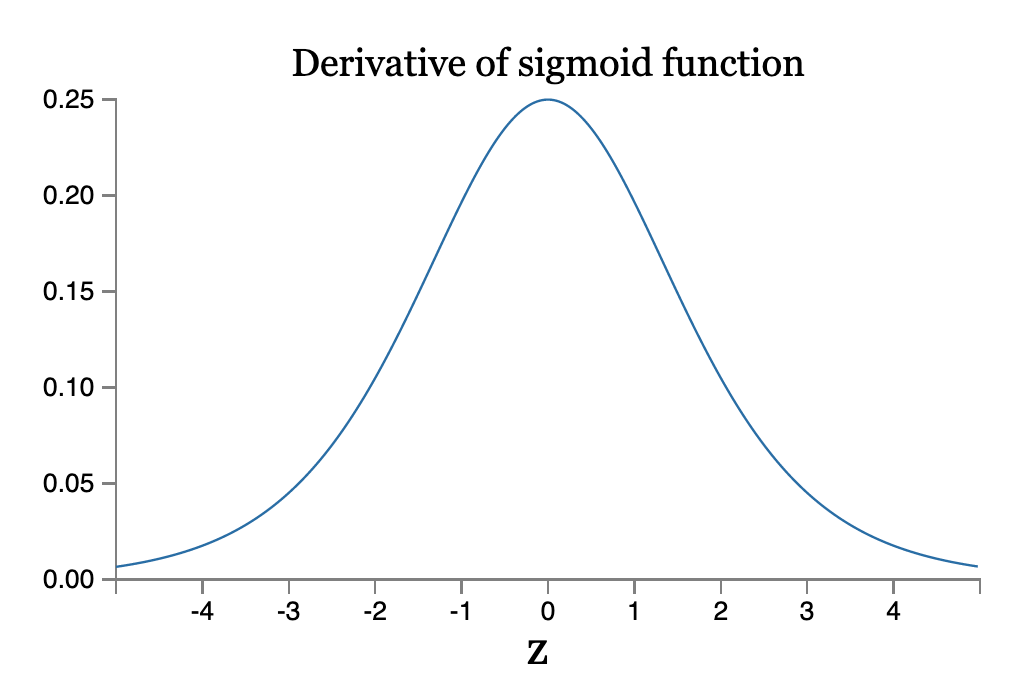
A derivada atinge um máximo em σ ′ (0) = 1/4. Agora, se usarmos nossa abordagem padrão para inicializar os pesos na rede, escolheremos os pesos usando uma distribuição normal (Gaussiana) com média 0 e desvio padrão 1. Assim, os pesos geralmente satisfazem | wj | < 1. Reunindo essas observações, vemos que os termos wjσ ′ (zj) geralmente satisfazem | wjσ ′ (zj) | < 1/4. E quando tomamos um produto de muitos desses termos, o produto tenderá a diminuir exponencialmente: quanto mais termos, menor será o produto. Isso está começando a cheirar como uma possível explicação para o problema da dissipação do gradiente.
Para tornar tudo isso um pouco mais explícito, vamos comparar a expressão para ∂C / ∂b1 com uma expressão para o gradiente em relação a um viés posterior, digamos ∂C / ∂b3. Naturalmente, não explicamos explicitamente uma expressão para ∂C / ∂b3, mas segue o mesmo padrão descrito acima para ∂C / ∂b1. Aqui está a comparação das duas expressões:
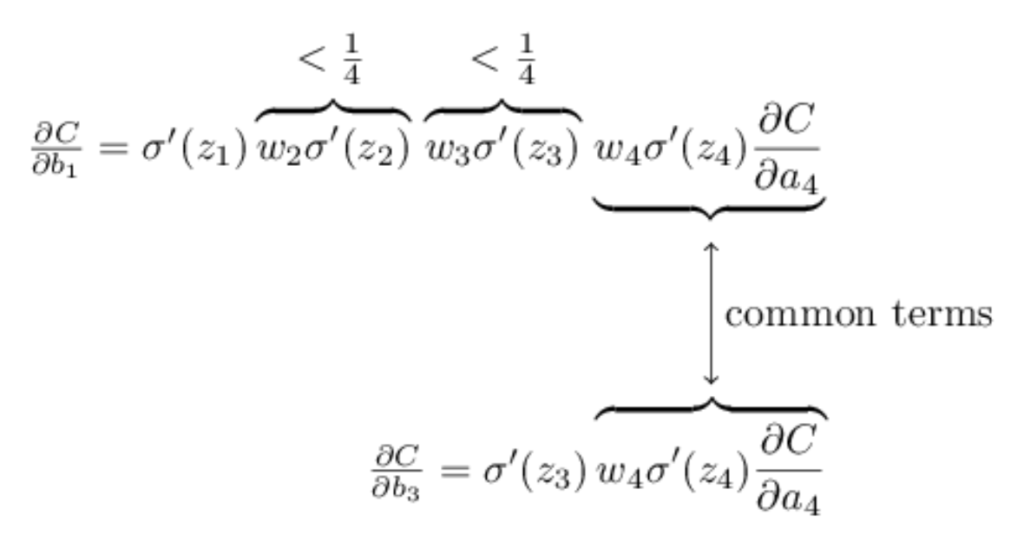
As duas expressões compartilham muitos termos. Mas o gradiente ∂C / ∂b1 inclui dois termos extras, cada um da forma wjσ ′ (zj). Como vimos, esses termos são tipicamente menores que 1/4 de magnitude. E assim o gradiente ∂C / ∂b1 normalmente será um fator de 16 (ou mais) menor que ∂C / ∂b3. Esta é a origem essencial do problema da dissipação do gradiente.
É claro que este é um argumento informal, não uma prova rigorosa de que o problema da dissipação do gradiente ocorrerá. Existem várias cláusulas de escape possíveis. Em particular, podemos nos perguntar se os pesos wj poderiam crescer durante o treinamento. Se o fizerem, é possível que os termos wjσ ′ (zj) no produto deixem de satisfazer | wjσ ′ (zj) | < 1/4. De fato, se os termos se tornarem grandes o suficiente – maiores que 1 – então não teremos mais um problema de dissipação do gradiente. Em vez disso, o gradiente crescerá exponencialmente à medida que nos movemos para trás pelas camadas. Em vez de um problema de dissipação do gradiente, teremos um problema de explosão do gradiente. Mas isso é assunto para o próximo capítulo!
Para aprender todos os detalhes matemáticos por trás desse processo, confira nosso curso único e exclusivo no Brasil: Matemática e Estatística Aplicada Para Data Science, Machine Learning e IA.
Até o próximo capítulo.
Referências:
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning (material usado com autorização do autor)
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

